Angoli interni ed esterni nei poligoni
Il concetto di angolo interno ed esterno per un poligono convesso è sufficientemente semplice e trattato in tutti i testi di geometria elementare. Richiamiamo qui le definizioni e proprietà fondamentali, solo per motivi di completezza.
Siano dati nel piano n (>2) punti
A1, A2, ...,
An, tali che tre consecutivi non siano in linea
retta e che la congiungente due a due dei punti, nell'ordine
in cui sono dati, lasci gli altri n-2 punti tutti in un
stesso semipiano. Si dice poligono
convesso la parte di piano comune agli angoli 
AnA1A
2, A1A2A3,
..., An-1AnA1.
Equivalentemente si può anche definire la stessa figura
come la parte di piano comune ai semipiani limitati dalle rette
A1A2,
A2A3,
...,AnA1 e contenenti
gli altri punti.
I punti A1, A2, ...,
An si dicono vertici del poligono, i
segmenti A1A2,
A2A3,
...,AnA1 si dicono
lati, gli angoli AnA1A2,
A1A2A3,
..., An-1AnA1
angoli interni, i 2n angoli ad essi adiacenti
si dicono angoli esterni. Si noti che ogni angolo
interno ha due angoli esterni ad esso corrispondenti. Ciascuno
dei segmenti che congiungono due vertici non consecutivi si dice
diagonale. Il numero delle diagonali di un poligono
è sempre 
(e la cosa rimane valida
anche con i poligoni non convessi che considereremo più
avanti).
E' tradizione, nel costruire gli angoli esterni di un poligono convesso, orientare il poligono stesso in uno dei due versi possibili e prendere, per ciascun angolo interno, come angolo esterno quello che ha come primo lato il prolungamento del primo lato dell'angolo interno e come secondo lato lo stesso secondo lato dell'angolo interno.
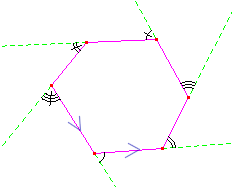
Si dimostra, come conseguenza immediata del teorema sulla somma degli angoli interni di un triangolo, che la somma degli angoli interni di un poligono convesso è uguale a tanti angoli piatti quanti sono i vertici, meno due. Conseguentemente la somma degli angoli esterni (considerandone uno per ogni vertice) è un angolo giro.
I problemi relativi agli angoli interni ed esterni sono molto più complessi nel caso di poligoni non convessi o, addirittura, intrecciati. Daremo qui solo un breve cenno del problema, rimandando a trattati più specialistici un approfondimento della questione (si può consultare, per esempio, Brusotti, L., Poligoni e Poliedri, in Enciclopedia delle matematiche elementari, II-I, Hoepli, Milano 1937)
Occorre innanzitutto modificare la definizione di poligono. Seguiremo la classica definizione di L.Poinsot:
Si dice poligono la figura
composta da n>2 punti A1,
A2, ..., An (detti
vertici) assunti ordinatamente nel piano e dei segmenti
(detti lati) che congiungono il primo con il secondo,
il secondo con il terzo, ..., l'ultimo con il primo. Se
esistono punti diversi dai vertici nei quali concorrono due o
più lati il poligono si dice intrecciato,
altrimenti si dice ordinario.
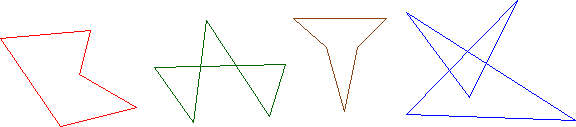
Nelle figure qui sotto sono rappresentati alcuni esempi di pentagoni: il primo e il terzo sono ordinari (ma non convessi), il secondo e il quarto sono intrecciati.
.
Per poter parlare di angoli interni ed esterni in questo caso più generale occorre innanzitutto orientare il piano: in senso intuitivo parleremo di orientamento orario ed antiorario (segnalando però che si tratta di concetti del tutto imprecisi!). Assumeremo, salvo avviso contrario, come positivo il verso antiorario. Orientato il piano si deve orientare anche, a piacere, il poligono, in uno dei due versi possibili. Per i poligoni ordinari (non intrecciati) si può scegliere (come noi faremo) di orientare anche il poligono in verso antiorario, mentre il concetto non ha più senso nel caso di poligoni intrecciati.
Considerato ora un angolo del poligono immaginiamo di far ruotare il secondo lato attorno al vertice in modo che descriva un angolo positivo (antiorario nella nostra convenzione) per sovrapporsi al primo lato: l'angolo descritto si chiamerà angolo interno. Si noti che, se si cambia il verso del poligono, ciascun angolo α si cambia in 2π-α.
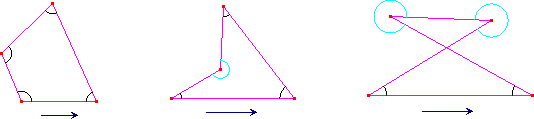
Nelle figure qui sotto sono rappresentati gli angoli interni (!) nei casi possibili per un quadrilatero (orientato in senso antiorario se è ordinario). Si noti come la somma degli angoli interni possa essere anche 2 angoli giri (nell'ultimo caso di figura).
Con le stesse convenzioni di prima diremo angolo esterno l'angolo (compreso tra -π e π) di cui deve ruotare il primo lato per sovrapporsi al secondo anche nel verso. In questo modo si mantiene una caratteristica valida per i poligoni convessi e cioè che la somma di un angolo interno coll'angolo esterno ad esso adiacente è sempre π.
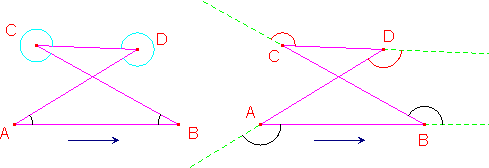
Nella figura qui sotto sono rappresentati gli angoli interni (a sinistra) e quelli esterni (a destra) relativamente ad un quadrilatero intrecciato. Gli angoli interni sono tutti positivi (due sono convessi e due sono concavi), mentre di quelli esterni due sono positivi (quelli di vertici A e B) e due negativi (quelli di vertici C e D). E' immediato verificare che la somma di ogni angolo interno coll'angolo esterno ad esso adiacente è π.
Come si può vedere da questi semplici esempi la situazione diventa assai complessa ed è per questo che nei testi elementari di geometria il concetto di angolo interno ed esterno di un poligono è limitato al caso di poligoni convessi. Solo per i più volenterosi riportiamo l'elenco delle situazioni (relativa agli angoli interni) che si possono presentare nel caso di un pentagono. Chi è veramente patito potrebbe provare con gli esagoni, tenendo conto che in questo caso per un punto diverso dai vertici possono passare anche tre lati diversi!