Funzioni periodiche
Definizione
Sia data una funzione reale di variabile reale, x
f(x). Se esiste un numero reale
p strettamente positivo, tale che, per ogni x
del dominio, x±p sta ancora nel dominio e che
f(x+p) = f(x), allora p si
dice un periodo per f.
Osservazioni
Si noti che, essendo f(x+2p) = f(x+p+p) = f(x+p) = f(x), se p è un periodo, anche 2p (e di conseguenza np, per ogni n naturale non nullo) è un periodo. Da ciò si può dedurre che il dominio della funzione non può essere limitato.
Si noti poi che, essendo f(x) = f((x-p)+p) = f(x-p), la definizione si può scrivere anche f(x±p) = f(x).
Geometricamente la definizione data implica che il grafico di una funzione periodica si può tracciare per ripetizione del grafico ottenuto restringendo il dominio ad un qualunque intervallo di ampiezza p. Il grafico qui sotto può rendere bene l'idea.
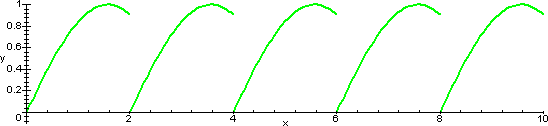
Esempi
- f(x) = k (funzione costante). Ogni numero reale positivo è, banalmente, un periodo per questa funzione.
- f(x) = sin(x). I numeri 2kπ, con k intero >0, sono periodi per la funzione.
- f(x) = sin(πx). I numeri naturali positivi pari sono periodi per la funzione.
- f(x) = sinx·cosx. I numeri kπ, con k intero >0, sono periodi per la funzione.
-
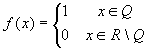. Tutti i numeri razionali strettamente
positivi sono periodi per la funzione. Basta, per provarlo,
osservare che la somma di due razionali è ancora un
razionale, mentre la somma di un razionale con un irrazionale
è ancora un irrazionale.
-
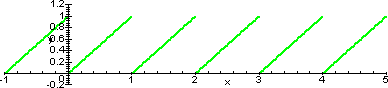
f(x) = x - [x] ([x] è la funzione
"parte intera", definita ponendo [x]
uguale al più grande intero non superiore ad
x; questa funzione è nota anche, soprattutto
nei linguaggi di programmazione, con il nome di
floor(x)). Questa funzione ha come periodi tutti i
numeri naturali strettamente positivi. Il suo grafico
è rappresentato qui sotto.
Come si vede dagli esempi, e come del resto si deduce dalla
definizione, una funzione in generale ha infiniti periodi.
Possiamo considerare l'insieme di tutti i periodi di una
funzione f, cioè: 
.
Può succedere che l'insieme A abbia un minimo oppure
no. Negli esempi precedenti il minimo esiste per le funzioni
numero 2 (minimo 2π), 3 (minimo 2), 4 (minimo π), 6
(minimo 1), mentre non esiste per gli esempi 1 e 5, dove invece
l'insieme A ha zero come estremo inferiore. Si dà
allora la seguente definizione:
Definizione
Sia data una funzione reale di variabile reale, xf(x) e si consideri l'insieme
. Il minimo di A, diciamolo T, se esiste,
si chiama minimo
periodo o, semplicemente, periodo della funzione
f e la funzione stessa si dice periodica di periodo
T. Se il minimo di A non esiste
la funzione non si dice periodica.
Le più importanti funzioni periodiche che si considerano in matematica sono le funzioni trigonometriche che hanno i seguenti periodi:
- sinx, cosx, secx, cosecx: 2π
- tanx, cotanx: π
La ricerca del periodo per le funzioni elementari
E' molto importante nelle applicazioni saper riconoscere le funzioni periodiche da quelle non periodiche ed eventualmente determinare il periodo. Purtroppo la cosa non è semplice e si trovano, anche su testi famosi o su siti web, molti strafalcioni.
Per le applicazioni più comuni ci si può limitare a considerare le funzioni trigonometriche e quelle ottenute da esse mediante somme, prodotti, quozienti o composizioni. Anche con questa limitazione comunque la verifica della periodicità e la ricerca dell'eventuale periodo non sono semplici.
Per renderci conto della difficoltà del problema, è opportuno considerare alcuni esempi.
Le
funzioni f(x) = sinx e g(x) = 1-sinx sono
entrambe periodiche di periodo 2π. La loro somma è
però la funzione costante h(x) = 1 che, come
osservato più sopra, non ha un minimo periodo e quindi
non viene considerata periodica. Un esempio simile si può
costruire con le funzioni f(x) = (sinx)2 e
g(x) = (cosx)2, la cui somma è 1.
Le due
funzioni f(x) = sinx e g(x) = sin(2x) - sinx
sono entrambe periodiche di periodo 2π. La loro somma
é la funzione h(x) = sin(2x) che è invece
periodica di periodo π.
Le due
funzioni f(x) = sinx e g(x) = sin(πx) hanno
periodo, rispettivamente, 2π e 2. La loro somma non è
nemmeno una funzione periodica. Discorso analogo vale per il
prodotto o il quoziente di queste due funzioni.
Le due
funzioni f(x) = sinx e g(x) = cosx sono
entrambe periodiche di periodo 2π. Il loro quoziente
è invece la funzione h(x) = tanx che
è periodica di periodo π. Discorso analogo sarebbe
vero per il prodotto.
Le due
funzioni f(x) = sinx e g(x) = 1 + cosx sono
entrambe periodiche di periodo 2π. Il loro quoziente è
la funzione h(x) = sinx/(1+cosx) che è ancora
periodica di periodo 2π.
La
funzione f(x) = sinx è periodica di periodo
2π. Il suo valore assoluto, g(x) = |sinx|, è
periodica di periodo π.
La
funzione f(x) = sinx + 2 è periodica di periodo
2π. Il suo valore assoluto, g(x) = |sinx+2|,
è ancora periodica di periodo 2π.
In generale non si possono stabilire regole per determinare il periodo delle funzioni, e purtroppo nemmeno regole per dedurre il periodo di funzioni ottenute mediante somme, prodotti o composizioni da altre funzioni periodiche. Ci si può solo attenere alle indicazioni di massima che seguono, che vanno però verificate caso per caso.
-
Se una funzione xf(x) è periodica di periodo T,
allora la funzione xf(kx), con k reale diverso da zero,
è periodica di periodo T/|k|.
- Se si hanno due funzioni periodiche con diverso periodo T1 e T2, e se esistono multipli interi comuni dei due periodi, allora le funzioni somma, prodotto, quoziente, hanno periodo uguale al minimo comune multiplo dei periodi. Un esempio in cui la regola non funziona è dato dal prodotto tra sinx e cos(3x), periodiche di periodo 2π e 2π/3, mentre il prodotto è periodico di periodo π, anche se il minimo comune multiplo dei periodi è 2π.
- Se si hanno due funzioni periodiche con lo stesso periodo T, allora le funzioni somma, prodotto, quoziente, hanno periodo minore o uguale al periodo comune T. Ci sono comunque eccezioni come quelle proposte nel primo esempio sopra riportato (ma ce ne sono anche altre più complesse).
Le funzioni periodiche giocano un ruolo fondamentale in tutte le applicazioni: basta pensare che la nostra vita è regolata da fenomeni sostanzialmente periodici come il battito del cuore (quando ci sono sbalzi nella durata del periodo ci si comincia a preoccupare!), l'alternarsi del dì e della notte, l'alternarsi delle stagioni, ecc.
Tra le funzioni periodiche giocano un ruolo essenziale, come già detto, quelle trigonometriche. Questa osservazione è molto più profonda di quanto non possa sembrare a prima vista: in sostanza le funzioni seno e coseno sono i modelli di base di tutte le funzioni periodiche, purché non troppo patologiche. Questo fatto è contenuto nell'importantissimo teorema di sviluppabilità di una funzione in serie di Fourier, di cui riportiamo qui solo l'enunciato in forma schematica.
Data una funzione sufficientemente regolare e periodica di
periodo 2π, vale, con qualche limitazione, la seguente
uguaglianza: 
. Questo vuol dire che tutte le
funzioni periodiche possono essere pensate, entro certi limiti,
come combinazioni delle funzioni seno e coseno. Tra le
applicazioni più famose di questo teorema citiamo la
scomposizione di un suono nei suoi armonici, scomposizione che
sta alla base dell'acustica musicale.