Il dominio di una funzione composta
Scopo di questa pagina è mostrare come si possa determinare, per via grafica, il dominio della funzione composta di due funzioni reali di variabile reale, a partire dal loro grafico.
Considerate due funzioni 
, si può
considerare la composta 
delle due se e solo se
l'immagine di g è contenuta nel dominio di
f. Se questo non succede si può sempre
considerare una restrizione di g a quei punti del suo
dominio che hanno immagine contenuta nel dominio di f.
É proprio questo che si fa abitualmente quando si
vuole determinare il "dominio
naturale" della composta di due funzioni reali,
espresse da determinate regole di calcolo matematico.
In questa pagina vogliamo provare che questa operazione si può fare anche semplicemente per via grafica.
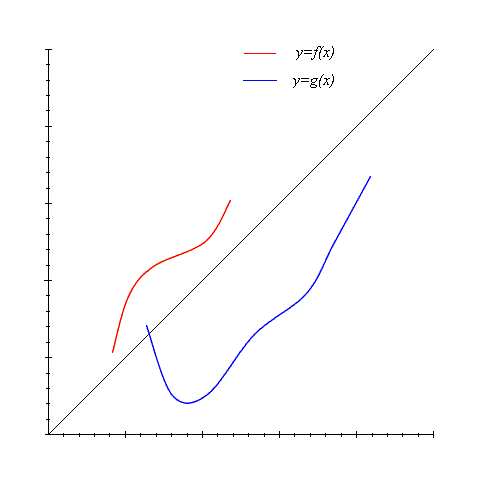
Cominciamo con l'osservare che il grafico della funzione f non ha alcun interesse, mentre hanno ovviamente interesse il dominio di g (l'insieme che vogliamo determinare è un sottoinsieme del dominio di g), il dominio di f (perché dobbiamo cercare le immagini di g che cadono dentro il dominio di f), e il grafico di g (che determina dove cadono le immagini di g).
Per risolvere il problema utilizzeremo la tecnica che permette di costruire graficamente la funzione composta di due funzioni, a partire dai loro grafici. Basta ora cliccare sui vari passi indicati qui sotto.
|
|
|
|
|
|
|
|
|
| uno | due | tre | quattro | cinque | sei | sette | otto | conclusioni |
