Taylor e dintorni - Qualche richiamo teorico
Algebra degli "o piccolo"
Ricordiamo innanzitutto la seguente definizione. Se
g(x) è una funzione diversa da zero in
un intorno di un punto c, escluso al più
c, e se f(x) è una funzione
tale che 
, allora si dice che f
è "o piccolo" di
g, per x tendente a c, e si usa
scrivere f(x) =
o(g(x)). Questa scrittura
intende suggerire l'idea che f è
"infinitamente piccola" rispetto a g.
La definizione ha interesse soprattutto nel caso in cui f e g siano entrambe infinitesime o entrambe infinite. Se sono entrambe infinitesime, dire che f è "o piccolo" di g equivale a dire che f tende a zero "più rapidamente" di g (cioè che un infinitesimo di ordine superiore); se sono entrambe infinite equivale a dire che f tende all'infinito "più lentamente" di g (cioè che è un infinito di ordine inferiore).
La definizione fu introdotta originariamente da Edmund Landau (1877-1938) ed è largamente usata, in particolare in relazione alla formula di Taylor. E' di uso comune la scrittura f(x) = h(x) + o(g(x)), al posto di f(x) - h(x) = o(g(x)).
E' molto importante ricordare che dire che f è "o piccolo" di g non dà alcuna informazione su come è fatta la funzione f, se non che il limite del rapporto tra f e g è zero. Si vedano gli esempi che seguono, in cui abbiamo considerato funzioni affatto diverse, ma tutte o(g), con la stessa g (verificarlo come esercizio!):
- ln(1+x2) = o(x), per x tendente a zero;
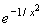- sinx - x = o(x), per x tendente a zero;
-
= o(x), per x tendente a
zero;
- 37x2 = o(x), per x tendente a zero;
- x2ln|x| = o(x), per x tendente a zero.
E' utile saper manipolare espressioni contenenti i simboli o piccolo, in particolare quando si deve lavorare con le approssimazioni di Taylor. Le situazioni più comuni nelle applicazioni sono quelle che riguardano il caso x tendente a zero e riassumiamo qui alcune delle regole di uso più frequente, di dimostrazione immediata.
- o(xm) ± o(xn) = o(xp), dove p è il minore tra m ed n;
- o(xm)·o(x n) = o(xm+n);
- xm·o(xn) = o(xm+n);
- xm = o(xn), se n < m.
Forniamo qualche esempio per chiarire il modo di procedere e il significato di queste scritture.
Esempio 1 x3 +
x5 = x3 +
o(x4) = x3 +
o(x3). Sia la prima che la seconda
uguaglianza scritte mi permettono di concludere che
x3 + x5, in un intorno
di zero, può essere approssimata con
x3 e, per esempio, che 
.
Esempio 2 x3 +
x5 = o(x2) +
o(x4) =
o(x2). Questa uguaglianza, se pur
corretta, non è di alcuna utilità, in quanto
afferma che la funzione a primo membro è infinitamente
più piccola di x2, ma non mi permette
di fare alcuna approssimazione della funzione stessa né,
per esempio, di calcolare 
con α>2.
Esempio 3 f(x) = x4 + o(x3) + x = o(x3) + o(x3) + x = o(x3) + x. E' utile osservare che le due uguaglianze relative alla funzione f: f(x) = x4 + o(x3) + x e f(x) = o(x3) + x, hanno esattamente lo stesso contenuto di informazioni.
Esempio 4 x + x5 + x7 + o(x3) + x2 + o(x6) = x + o(x3) + o(x3) + o(x3) + x2 + o(x6) = x + x2 + o(x3).