Sviluppi di Taylor non elementari
Esercizio 1 Trovare lo sviluppo di Taylor di ordine 5 di (sinx)2 - sin(x2).
Si deve fare in modo che facendo la differenza tra gli sviluppi di (sinx)2 e sin(x2), non si "semplifichino tutti i termini che precedono gli o piccolo". Mentre è immediato valutare i termini dello sviluppo di sin(x2), per il quale basta sostituire x con x2 nello sviluppo di sinx, non è altrettanto immediato il calcolo dello sviluppo di (sinx)2, per ottenere il quale occorre elevare al quadrato lo sviluppo di sinx. Si possono fare alcuni di tentativi dopodiché, di solito, si riesce a concludere.
Si ha: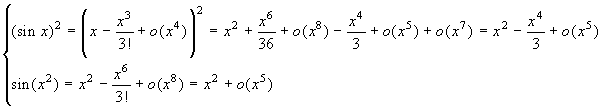 
. Se ne deduce che: 
.
Naturalmente lo sviluppo poteva anche essere trovato per via
diretta calcolando le derivate successive fino alla quinta. Si
verifica, con un po' di pazienza, che 
e che
tutte si annullano, mentre 
. Da qui si ottiene
nuovamente il risultato precedente.
Esercizio 2 Trovare lo sviluppo di
Taylor di ordine 4 di 
.
Si può partire dallo sviluppo di
(1+t)1/4. Si ha: 
.
Sostituendo x4-4x2 al
posto di t si trova 
.
Esercizio 3 Trovare lo sviluppo di
Taylor di ordine 4 di 
.
Partendo dallo sviluppo di (1+t)1/2, si
trova: 
. Sostituiamo
sin2x al posto di t: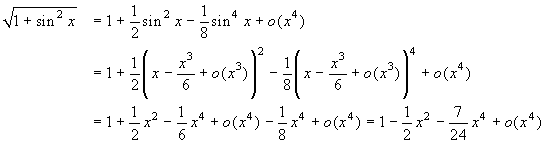 
.
Esercizio 4 Dopo aver provato che la funzione f(x) = x - e-x è invertibile, calcolare lo sviluppo di Taylor di ordine 2 della funzione inversa, di punto iniziale -1.
L'invertibilità della funzione discende
immediatamente dal fatto che la sua derivata è sempre
strettamente positiva. Si ha inoltre f(0) = -
1. Dobbiamo calcolare le derivate prima e seconda
dell'inversa. Usando la nota regola di derivazione troviamo:
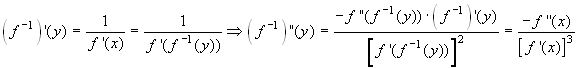. Allora: 
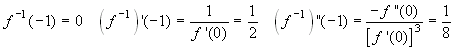. Lo sviluppo richiesto
per la funzione inversa è: 
.
Esercizio 5 Data la funzione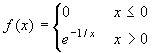 
, si dimostri che essa ammette polinomi di Taylor di
qualunque ordine, di punto iniziale 0, e si determinino tutti
questi polinomi. Si trovi un'altra funzione che ha gli
stessi polinomi di Taylor di f, di qualunque ordine.
Si tratta di provare che la funzione ammette derivate di
qualunque ordine. La continuità è ovvia, visto che
il limite in zero è zero. Controlliamo la
derivabilità. Ovviamente per x < 0 la
derivata è identicamente nulla. Per x > 0 si
trova invece facilmente: 
. Se ne deduce che la
funzione ha anche la derivata prima e che essa si annulla
nell'origine. Possiamo passare alla derivata seconda, per
x > 0: 
. Dunque la funzione ha
anche la derivata seconda in zero e questa vale zero. Sia la
derivata prima che la derivata seconda, per x > 0,
si presentano nella forma 
, ove k
è un naturale e p(x) è un
polinomio, di grado minore di k. Ci viene il sospetto
che questa situazione si verifichi per tutte le derivate: lo si
può facilmente provare per induzione. Allora tutte le
derivate saranno nulle nell'origine e tutti i polinomi di
Taylor saranno identicamente nulli. Anche la funzione
identicamente nulla ha, ovviamente gli stessi polinomi. Per la
funzione f i polinomi di Taylor non servono
assolutamente a nulla!