Esercizi su approssimazioni con la formula di Taylor - 1
Esercizio 1 Calcolare 
in modo che l'errore nell'approssimazione sia minore di
0.01.
Si possono seguire diverse strade:
- usare lo sviluppo di Taylor di (1+x)1/2, con punto iniziale 0, e valutare l'errore con x = e-1;
- usare lo sviluppo di Taylor di di (x)1/2, con punto iniziale 1, e valutare l'errore con x = e.
- usare lo sviluppo di Taylor di ex, con punto iniziale 0, e valutare l'errore con x = 1/2;
Valutiamo i pro e i contro delle diverse soluzioni proposte.
- Se usiamo lo sviluppo di Taylor di (1+x)1/2, con punto iniziale 0, nella valutazione dell'errore dobbiamo tenere conto che compare il fattore |x|n+1 = |e-1|n+1, valore che cresce al crescere di n, in quanto la base è maggiore di 1.
- Per usare lo sviluppo di Taylor di di (x)1/2, con punto iniziale 1, dovremmo prima calcolare questo sviluppo, che non è compreso tra quelli usualmente considerati fondamentali. Questo fatto però non crea problemi, in quanto basta sostituire x con x-1 nello sviluppo di (1+x)1/2. Rimane però valida l'osservazione fatta qui sopra, in quanto ora nel resto compare il fattore |x-1|n+1, che, valutato in x = e, dà sempre |e-1|n+1.
- Se usiamo lo sviluppo di Taylor di ex, con punto iniziale 0, nella valutazione dell'errore compare sempre il fattore |x|n+1, che però deve essere ora valutato in 1/2, e quindi decresce al crescere di n. Sembra questa essere la scelta più conveniente. C'è anche da tenere conto che utilizzando questo sviluppo i vari addendi del polinomio vengono calcolati su un valore razionale (1/2) e quindi il valore approssimato si può esprimere mediante frazioni.
Scriviamo dunque la formula di Taylor di punto iniziale 0,
relativa alla funzione esponenziale, e ponendo x = 1/2:
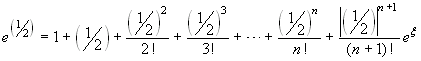. Poiché 0<ξ<(1/2),
eξ ≤ e1/2.
Inoltre, essendo e minore di 4, ne segue che
e1/2 < 2. L'errore sarà
maggiorato da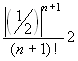 
. Basterà trovare
n tale che 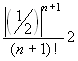sia minore di 0.01 (una
maggiorazione più grossolana si poteva ottenere
osservando che e1/2 ≤ e ≤ 3).
Si tratterà di trovare n tale che
(n+1)! ≥ 100. Se n=1 si ha
2·2=4<100, se n=2 si ha 6·4=24<100,
se n=3 si ha 24·8=192>100. Basterà
dunque prendere il polinomio di grado 3 e si ottiene: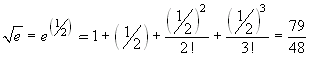 
.
Se si fosse considerato un polinomio di grado 4 l'approssimazione, probabilmente, sarebbe stata ancora migliore (211/128). Ci si può rendere conto di questo confrontando il valore di e1/2 con dieci cifre decimale esatte con quelli ottenibili con polinomi di diverso grado:
- e1/2 con dieci cifre decimali esatte: 1.6487212707...;
- polinomio di grado 3: 79/148 = 1.645833333... (due cifre decimali esatte, come richiesto);
- polinomio di grado 4: 211/128 = 1.6484375 (tre cifre decimali esatte);
- polinomio di grado 5: 6331/3840 = 1.648697916... (ancora tre cifre esatte);
- ...
Si noti come il passaggio da un grado al successivo non comporti necessariamente l'aumento del numero di cifre esatte.
Esercizio 2 Calcolare ln(1.2) in modo che l'errore sia minore di 0.001.
Si può usare lo sviluppo di ln(1+x) di punto
iniziale 0, con x = 0.2. Si tratta di trovare un valore
di n in modo che 
; poiché 
, basterà che 
ovvero
.
Se n=1 si ha 2·25=50<1000, se n=2 si
ha 3·125=375<1000, se n=3 si ha
4·625=2500>1000. Dunque il polinomio di grado 3 va
bene. Si ha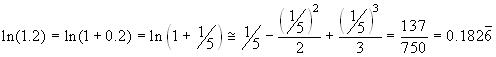 
. Il valore richiesto, con 10 cifre
decimali esatte, è: 0.1823215567; questo conferma la
correttezza del risultato trovato.
Esercizio 3 Calcolare 91/3, con un errore minore di 1/105.
Osserviamo che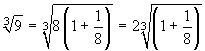 
: potremo usare lo
sviluppo di (1+x)α, con α=1/3 e
x = 1/8. Dovremo trovare n in modo che
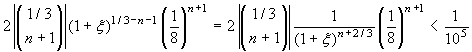. Poiché 0<ξ<1/8, 
:
potremo limitarci a cercare n tale che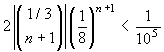 
.
Se n=1 l'errore massimo è 1/288; se
n=2 l'errore massimo è 5/20736, se
n=3 l'errore massimo è 5/248832, se
n=4 l'errore massimo è 11/5971968 e
l'ultimo valore soddisfa le richieste del problema. Potremo
dunque concludere con la seguente uguaglianza approssimata: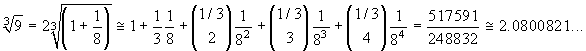 
Per un utile confronto si può calcolare il
valore richiesto (mediante un software di calcolo automatico!),
con dieci cifre decimali esatte; si ottiene 2.0800838230..., in
perfetto accordo con quanto da noi trovato.
Esercizio 4 Calcolare ln(0.5) con un errore minore di 10-2.
Si può usare la formula di Taylor di ln(1+x), di
punto iniziale 0, valutata per x = -1/2. Dobbiamo
trovare n in modo 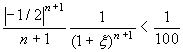che 
. Poiché -1/2
< ξ < 0 basterà trovare n tale che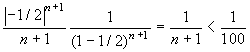 
. Si deduce subito che il minimo valore di
n è 100. Dunque per ottenere un valore
approssimato a meno di 1/100 di ln(0.5) occorre calcolare 
, cosa non proprio agevole (per pura
curiosità riportiamo il risultato 
, che
abbiamo ottenuto con Derive™). Naturalmente non è
affatto escluso che in questo risultato l'errore sia anche
minore di 1/100, in quanto noi abbiamo trovato solo l'errore
massimo, che si ha in corrispondenza di ξ=-1/2. Purtroppo noi
non abbiamo alcuna indicazione su quanto vale ξ, tranne il
fatto che -1/2 < ξ < 0: se per caso questo valore fosse
molto vicino a zero potrebbero bastare molti meno addendi per
avere l'approssimazione richiesta.
Si può osservare che se prendiamo x = 1/2,
ovvero se cerchiamo un valore approssimato di ln(1.5),
l'errore è dato da 
, valore maggiorato
da 
, in quanto ora 0 < ξ < 1/2.
Affinché questo errore sia minore di 1/100 basta ora
prendere n = 4 e il valore approssimato di ln(1.5)
è semplicemente 77/192. Il motivo di questa differenza di
comportamento tra 1/2 e -1/2 è che -1/2 sta molto
"più vicino all'asintoto verticale" di
ln(1+x) che non 1/2.
Esercizio 5 Calcolare sin(1) con un errore minore di 10-10.
Se utilizziamo lo sviluppo di Taylor di ordine 2n di
sin(x), di punto iniziale 0, con x = 1,
troviamo per il resto la maggiorazione: 
. Se
vogliamo che questo valore sia minore di 10-10,
basterà trovare n in modo che
(2n+1)!>1010. Calcolando il primo membro
troviamo per n = 6 (2*6+1)!=6.227.020.800, mentre per
n = 7 (2*7+1)!=1.307.674.368.000. il primo valore
valido è dunque n =7. Il valore cercato si
ottiene dunque dalla seguente somma: 
. Il
valore approssimato fino alla 15 cifra decimale (ottenuto con
Derive™) è: 0.841470984807896...: come si vede
l'obiettivo è stato perfettamente raggiunto.
Dal punto di vista del calcolo dell'errore sarebbe stato
molto più conveniente utilizzare lo sviluppo di
sin(x) con punto iniziale π/2, in quanto 1 è
più vicino a π/2 che non a 0. Questo sviluppo si trova
facilmente se si tiene conto che le prime quattro derivate della
funzione seno sono, nell'ordine, cosx,
-sinx, -cosx, sinx, e successivamente
si ripetono. Si trova dunque: 
. il resto
R2n(x) è maggiorato da 
.
Nel nostro caso in cui x vale 1, se teniamo conto conto
che π/2<1.6, possiamo concludere che tale resto si
può maggiorare con 
, un valore decisamente
inferiore, in particolare per n grande, rispetto al
precedente: basterà un polinomio di grado molto minore
per ottenere lo stesso livello di approssimazione. Se questa
è una facilitazione, bisogna però tenere conto che
per calcolare i vari addendi del polinomio di Taylor in
x=π/2 occorre valutare π con un elevato numero di
cifre decimali esatte, per evitare che gli errori di
arrotondamento introdotti nei calcoli facciano sensibilmente
diminuire la precisione del risultato che si ottiene.