Esercizi sui limiti anche con la formula di Taylor
Esercizio 1 
.
Utilizzando la formula di Taylor e i limiti fondamentali si
conclude che:
-
;
-
;
-
;
-
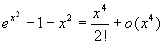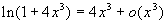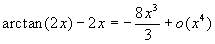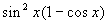è un infinitesimo di ordine 4.
Se ne deduce che il limite può essere ridotto a 
.
Esercizio 2 Calcolare, al variare di
β>0, il limite seguente: 
.
Utilizzando la formula di Taylor ricaviamo che:
-
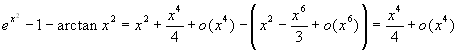, da cui 
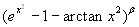è un
infinitesimo di ordine 4β.
-
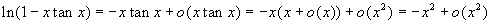, per cui ln(1-xtanx)
è un infinitesimo di ordine 2 (la cosa è anche
una conseguenza immediata dei limiti fondamentali).
Allora:
- se 4β>2 al numeratore rimane solo -ln(1-xtanx);
-
se 4β<2 al numeratore rimane solo;
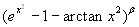- se 4β=2, nessuno dei due addendi del numeratore può essere trascurato.
Esaminiamo separatamente i 3 casi.
-
β>1/2. Si ha:
.
-
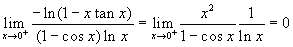β<1/2. Si ha:
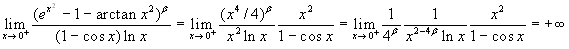(si è tenuto
conto del fatto che 2-4β>0).
-
β<1/2. Con alcune manipolazioni algebriche il limite
si può scrivere nella forma seguente:
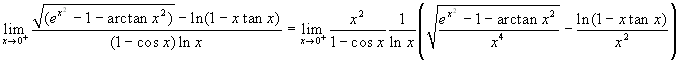. Tenendo conto di quanto sopra ricavato il primo
addendo entro parentesi ha limite 1/2, il secondo -1. Il
primo dei tre fattori ha poi limite finito. Il risultato
finale è dunque 0.
Esercizio 3 Calcolare, al variare
di β>0, il limite seguent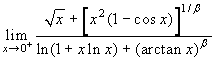e: 
.
Utilizzando la formula di Taylor e/o limiti fondamentali
ricaviamo che:
-
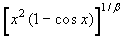è un infinitesimo di ordine
4/β, mentre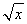 
è di ordine
1/2;
- (arctanx)β è un infinitesimo di ordine β;
- ln(1+xlnx) è un infinitesimo di ordine minore di 1 (è un ordine "infrareale" strettamente minore di 1, ma strettamente maggiore di ogni reale inferiore ad 1).
Allora:
- al numeratore dovremo distinguere tre casi a seconda che 4/β sia maggiore, minore, uguale a 1/2, ovvero a seconda che β<8, β>8, β=8;
- al denominatore dovremo distinguere due casi a seconda che β sia minore di 1 oppure maggiore o uguale ad 1.
Esaminiamo separatamente le varie situazioni:
-
β<1. Si ha
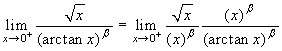. A questo punto
dovremo ancora distinguere tre casi a seconda che
β<1/2, β=1/2, β>1/2. Nel primo caso il
limite è 0, nel secondo caso è 1, nel terzo
caso è +∞.
-
1≤β<8. Si ha
.
-
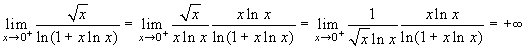β=8. Il limite diventa:
-
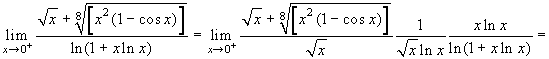
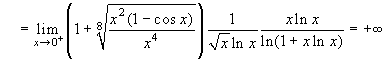
β>8. Rimane
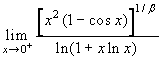. Poiché il
numeratore è infinitesimo di ordine 4/β<1/2,
mentre il denominatore non ha ordine, ma è sicuramente
>1/2, il limite è +∞.
Esercizio 4 
.
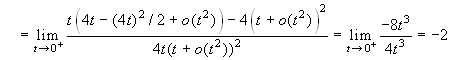Esercizio 5 
. Al
denominatore abbiamo la somma di due infinitesimi, di cui il
primo è di ordine 3, il secondo è infrareale, ma
minore di 3. Si può dunque trascurare il primo addendo.
Al numeratore si può applicare la formula di Taylor: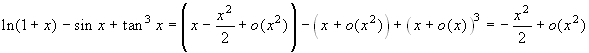 
. Rimane dunque 
.