Esercizi sui limiti con infinitesimi, infiniti e regola di l'Hôpital
Esercizio 1 
. Questo
esercizio è interessante perché, nonostante la sua
apparente semplicità, non è risoluzione facilmente
senza l'uso della regola di l'Hôpital (o della
formula di Taylor). Si può invece, solo con i limiti
fondamentali, calcolare 
. Si noti la differenza
nel risultato rispetto al limite precedente, anche se, in un
intorno di zero, le funzioni tanx ed x si
possono ritenere sostanzialmente coincidenti.
Esercizio 2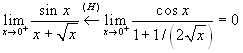 
.
Oppure: 
.
Oppure: 
(si è sfruttato il fatto che
x è infinitesimo di ordine superiore a 
).
Esercizio 3 
(applicare l'Hôpital all'argomento
dell'esponenziale).
Esercizio 4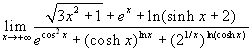 
.
Esaminiamo separatamente i vari addendi che compaiono al
numeratore e al denominatore. 
e 
sono infiniti di ordine 1 e tale è anche la loro somma
(lo si può verificare facilmente con un calcolo diretto).
Al numeratore predomina dunque ex, e il
resto si può trascurare (è o piccolo di
ex). Al denominatore 
e 
sono funzioni limitate (la prima ovviamente, per
la seconda basta scrivere l'esponente nella forma 
, che tende ad 1). Rimane dunque solo 
.
Si può ora calcolare il limite seguente: 
.
All'esponente x è un infinito di ordine 1,
mentre ln(x)ln(coshx) è di ordine
maggiore di 1 (è il prodotto tra ln(coshx), che
è di ordine 1, per lnx che è un
infinito).
Esercizio 5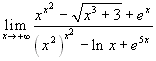 
.
Esaminiamo separatamente i vari addendi che compaiono al
numeratore e al denominatore. Sia al numeratore che al
denominatore ci sono tre infiniti di ordine diverso e
chiaramente il primo è quello di ordine maggiore in
entrambi i casi (basta scriverli nella forma 
ed 
per rendersene conto).
Il limite che rimane è facilmente calcolabile: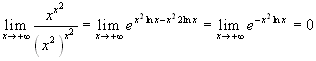 
.
Esercizio 6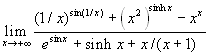 
.
Esaminiamo separatamente i vari addendi che compaiono al
numeratore e al denominatore. Si ha 
; poi
è chiaramente di ordine superiore rispetto
a 
. Al denominatore il primo ed il terzo addendo non
sono infiniti. Rimane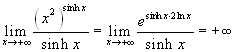 
(il numeratore è
chiaramente di ordine superiore al denominatore).
Esercizio 7 
. Al
denominatore abbiamo la somma tra un infinito e una funzione
limitata, che dunque si può trascurare. Al numeratore
abbiamo la somma tra due infiniti. Ne facciamo il confronto,
calcolando il limite del rapporto: 
. Se ne
deduce che xex si può trascurare.
Rimane allora da calcolare 
. Il numeratore è
un infinito di ordine maggiore di ex, mentre
il denominatore è dello stesso ordine di
ex. Se ne deduce che il limite è
-∞.
Esercizio 8 
. Per il secondo fattore si è fatto uso di
.
Esercizio 9 
.
Calcoliamo il limite dell'esponente. Si ha: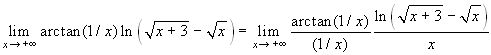 
.
Il primo fattore tende ad 1, per il secondo si ha: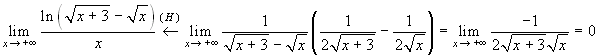 
. Il limite vale 1.
Esercizio 10 Sia f una
funzione continua con le sue derivate, almeno fino
all'ordine 3. Supposto che f(0)=0 e
f"(0)≠0, calcolare: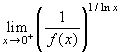 
. Il
limite si può trasformare in 
. Si
può considerare solo l'esponente, applicando la
regola di l'Hôpital. 
. Si può ora
osservare che f' non può essere nulla in
tutto un intorno di 0, perché altrimenti
f"(0)=0. Allora se f'(0)≠0
l'esponente tende a -1 e il limite vale 1/e; se
invece f'(0)=0 il limite si presenta ancora nella
forma 0/0 e si può di nuovo applicare la regola di
l'Hôpital: 
. Il limite vale allora
1/e2.
Esercizio 11 
.
Esaminiamo l'esponente: 
. A questo punto
l'applicazione della regola di l'Hôpital fornisce
subito il valore zero per il limite dell'esponente. In
definitiva il limite richiesto è 1.