Esercizi sulla continuità uniforme
Esercizio 1 Dire se la funzione f(x)=arctanx/x è uniformemente continua in ]0,+∞[.
Osserviamo che si ha 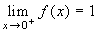 e
e 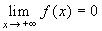 . Se ne deduce che la funzione è
prolungabile per continuità a tutto [0,+∞[ e che,
avendo un asintoto orizzontale, è ivi uniformemente
continua. A fortiori sarà uniformemente continua in
]0,+∞[.
. Se ne deduce che la funzione è
prolungabile per continuità a tutto [0,+∞[ e che,
avendo un asintoto orizzontale, è ivi uniformemente
continua. A fortiori sarà uniformemente continua in
]0,+∞[.
Esercizio 2 Si consideri la funzione
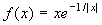 . Si dica
se è prolungabile per continuità a tutto
R e se la funzione prolungata è
uniformemente continua.
. Si dica
se è prolungabile per continuità a tutto
R e se la funzione prolungata è
uniformemente continua.
Poiché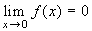 , la funzione è prolungabile per
continuità in 0, ponendo f(0)=0. La funzione
così ottenuta è continua su R ed
ha due asintoti obliqui: y = x+1 a +∞ e y =
x-1 a -∞, pertanto è uniformemente continua su
R.
, la funzione è prolungabile per
continuità in 0, ponendo f(0)=0. La funzione
così ottenuta è continua su R ed
ha due asintoti obliqui: y = x+1 a +∞ e y =
x-1 a -∞, pertanto è uniformemente continua su
R.
Esercizio 3 Provare che se una funzione è uniformemente continua in [a,b] e in [b,c], allora è uniformemente continua anche in [a,c].
Fissato ε>0, si considera ε/2 e, in
corrispondenza ad esso si trovano δ1 e
δ2 adatti per il primo e il secondo intervallo;
se δ è il più piccolo dei due esso va
bene per entrambi gli intervalli. Se ora x ed
y sono entrambi in uno dei due intervalli non ci sono
problemi; se invece essi sono uno nel primo e uno nel secondo si
può osservare che |x-y|<δ implica
|x-b|<δ e |b-y|<δ. Allora
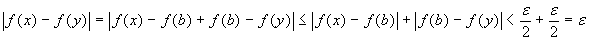 .
.
Esercizio 4 Provare per verifica
diretta che 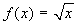 è uniformemente continua su
[0,+∞[.
è uniformemente continua su
[0,+∞[.
Si comincia con il provare che, per x ed y non
negativi, 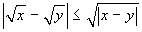 .
Si ha infatti, successivamente:
.
Si ha infatti, successivamente:
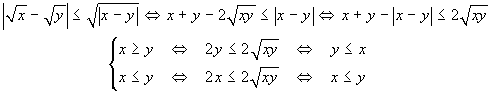 .
.
Se allora si prende δ=ε2, si può subito concludere.
Naturalmente si poteva anche osservare che sull'intervallo [0,1] la funzione è uniformemente continua per il teorema di Heine-Cantor, sull'intervallo [1,+∞[ è uniformemente continua perché ha derivata limitata. E' facile poi concludere con l'uniforme continuità sull'unione dei due intervalli. Infatti
Esercizio 5 Siano date due funzioni uniformemente continue f: A → R e g: B → R, tali che f(A)B. Mostrare che g°f è uniformemente continua.
Sia dato ε>0; è allora possibile trovare η>0 tale che da |y1-y2|<η segue |g(y1)-g(y2)|<ε; inoltre, a partire da η, è possibile trovare δ>0 tale che da |x1-x2|<δ segue |f(x1)-f(x2)|<η. Si può quindi concludere che, a partire da ε>0, è possibile trovare δ>0 tale che da |x1-x2|<δ segue |g(f(x1))-g(f( x2))|<ε. Questo basta per concludere.
Esercizio 6 Mostrare che una funzione continua e periodica di R in R è uniformemente continua.
Detto T il periodo, è sufficiente considerare un intervallo [a,b] tale che b-a = T: qui la funzione è uniformemente continua per il teorema di Heine-Cantor. Per il resto basta applicare la periodicità.
Esercizio 7 Provare che se f
è integrabile in [a,b], allora 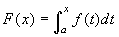 è Lipschiziana in [a,b].
è Lipschiziana in [a,b].
Basta osservare che 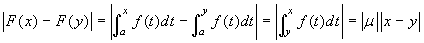 , dove l'ultima uguaglianza esprime il
teorema della media.
, dove l'ultima uguaglianza esprime il
teorema della media.