Esercizi su continuità e derivabilità - 1
Esercizio 1 E' data la funzione
.
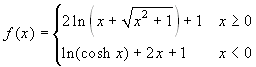- si verifichi che è di classe C1(R);
- si verifichi che è invertibile in R;
- detta g l'inversa si calcoli g'(1).
Cerchiamo intanto la derivata di f fuori
dall'origine: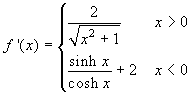 
.
Un calcolo immediato prova che la funzione è continua
nell'origine, dove vale 1, ed è anche derivabile con
continuità, con derivata 2. La derivata è inoltre
sempre positiva (si ricordi che la tangente iperbolica è
sempre >-1), per cui la funzione è invertibile.
Poiché si ha, come già osservato, f(0)=1,
se ne deduce che 
.
Qui sotto è rappresentato il grafico della funzione f.
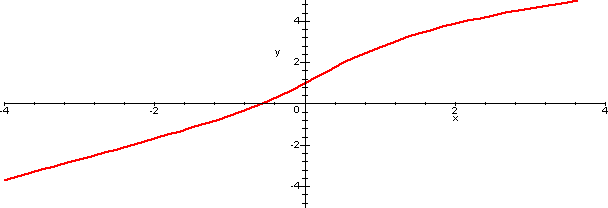
Esercizio 2 Si verifichi che, per x≠0, vale l'identità:
.
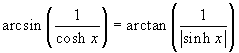Se si calcolano le derivate delle due funzioni a primo e secondo
membro si trova che entrambe valgono: 
. Dunque
sia sulla semiretta x<0 che su quella
x>0 le due funzioni possono solo differire per una
costante. Basterà calcolarne il valore in un punto sulla
prima semiretta e in uno sulla seconda per controllare se sono
uguali. Ancora più semplicemente si può provare a
fare, per entrambe, il limite al tendere a zero di x;
poiché questi limiti valgono π/2, si può
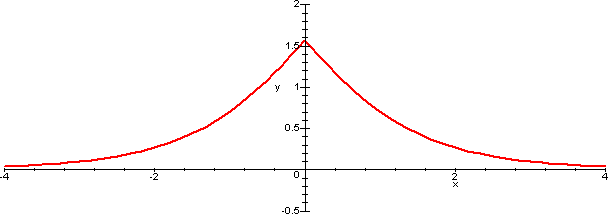
concludere che le funzioni coincidono. Il loro grafico comune
è rappresentato di seguito.
.
Esercizio 3 Determinare i valori di α per cui la funzione
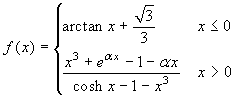
è continua in zero.
Intanto si ha 
. Calcoliamo ora il
limite destro in zero. Cominciamo con l'osservare che
. Se α=0 il numeratore si riduce a
x3, il limite destro vale 0 e la funzione
non è continua. Se α≠0 si ottiene: 
e il limite destro vale α2. la funzione
è continua se 
.
Si veda il grafico di seguito corrispondente al valore positivo di α.
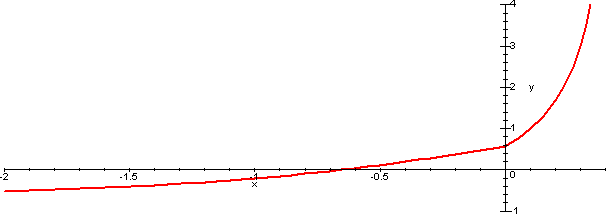
Esercizio 4 Data la funzione
,
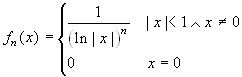dire se esiste n >0 tale che fn risulti derivabile nel suo dominio.
L'unico problema si ha per x=0, dove tutte le
fn sono continue. Per la derivabilità
calcoliamo il limite del rapporto incrementale.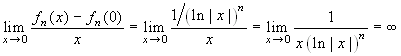 
.
Nessuna funzione può essere derivabile.
Esercizio 5 Sia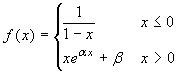 
.
Trovare α e β affinché la funzione sia di classe C1(R) e inoltre abbia limite 1 a +∞. In queste condizioni la f è C2(R)?
Cerchiamo la derivata fuori dall'origine. Si ha:
.
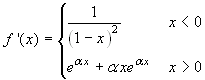La funzione è di classe C1(R)
per β=1 e per ogni α. Inoltre il limite a +∞
è 1 solo se 
, il che richiede
α<0. Per vedere se è di classe
C2(R) calcoliamo la derivata seconda
fuori dall'origine: 
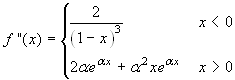. Poiché il
limite sinistro vale 2 e quello destro 2α, essi non
potranno essere uguali in quanto α<0.
Qui di seguito è rappresentato il grafico relativo al valore α=-1
