Un esempio complesso
L'esempio proposto in questa pagina è preso da Gorni
Gianluca, Polinomi di Taylor: illustrazioni, reperibile
in http://www.dimi.uniud.it/~gorni/.
Si tratta di un esempio costruito a partire dalla funzione 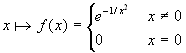 .
.
Si consideri la funzione 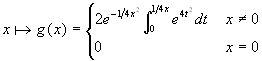 . Si può provare che essa è indefinitamente
derivabile in R e che il suo polinomio di
Taylor di punto iniziale 0, di ordine n = 2k+1
è:
. Si può provare che essa è indefinitamente
derivabile in R e che il suo polinomio di
Taylor di punto iniziale 0, di ordine n = 2k+1
è:
![]() .
.
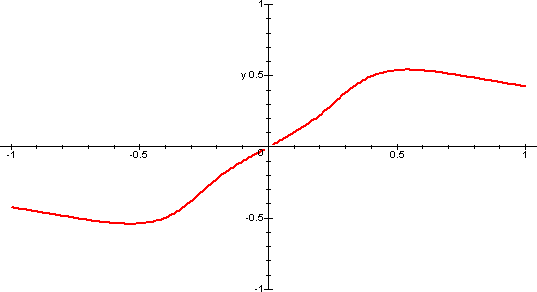
Utilizzando i link sottostanti puoi visualizzare la funzione g(x) (in rosso) e i polinomi approssimanti di diverso ordine (in blu), verificando che, all'aumentare del grado del polinomio, il grafico si "adagia" sul grafico di g(x) su un intervallo che si restringe al crescere del grado del polinomio. In questo caso dunque all'aumentare del grado la bontà dell'approssimazione polinomiale peggiora sempre di più.
|
|
|
|
|
|
|
|
| uno | due | tre | quattro | cinque | sei | sette |