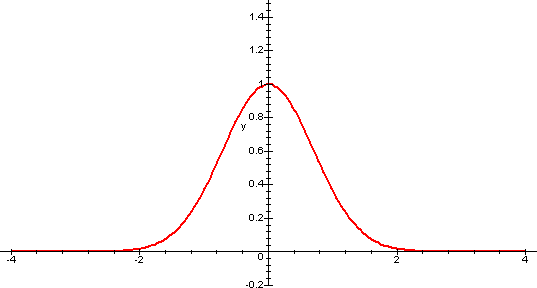
La funzione exp(-x2)
Per la funzione x 
exp(-x2) il polinomio di Taylor, di ordine
n = 2k si ottiene facilmente sostituendo
(-x2) al posto di x nel polinomio
relativo ad ex:
.
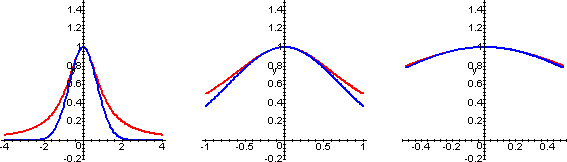
Utilizzando i link sottostanti puoi visualizzare la funzione exp(-x2) (in rosso) e i polinomi approssimanti di diverso ordine (in blu), verificando che, all'aumentare del grado del polinomio, il grafico si "adagia" sempre meglio e su un intervallo sempre più grande sul grafico della funzione exp(-x2).
|
|
|
|
|
|
|
| uno | due | tre | quattro | cinque | sei | sette |
E' molto interessante confrontare i risultati che si
ottengono per questa funzione, dove l'approssimazione con i
polinomi di Taylor è del tutto soddisfacente in quanto
all'aumentare del grado aumentano sia la precisione di
approssimazione sia l'intervallo in cui
l'approssimazione è "buona", con i
risultati ottenuti per la funzione x 1/(1+x2), dove invece
l'accettabilità dell'approssimazione rimane
"confinata" ad un intervallo limitato, senza
estendersi al dominio della funzione. La differenza drastica di
comportamento è tanto più significativa se si
esaminano i grafici qui sotto che provano che l'andamento
essenziale dei grafici delle due funzioni, è molto
simile. La differenza di comportamento può essere
compresa solo ragionando sul campo complesso, dove si vede che
la funzione z
1/(1+z2) ha due "poli" nei punti
±i, mentre la funzione z exp(-z2) non ha poli.
