Introduzione al problema
Nello studio delle funzioni reali di variabile reale i polinomi costituiscono un modello di primaria importanza perché le operazioni coinvolte nella loro definizione sono solo le due operazioni fondamentali di somma e prodotto. Tutti i problemi di calcolo di limiti, derivate, integrali di Riemann per questo tipo di funzioni hanno una soluzione molto semplice. E', tra l'altro, importante che l'insieme dei polinomi è "chiuso" rispetto alle operazioni di derivazione e antiderivazione: la derivata o una primitiva di un polinomio è sempre un polinomio. La cosa non è più vera quando si passa alle funzioni razionali fratte, dove per esempio una primitiva di 1/x è lnx, cioè una funzione trascendente.
Probabilmente però la ragione primaria della centralità delle funzioni polinomiali sta nella formula di Taylor, che consente l'approssimazione, almeno localmente, di tutte le funzioni sufficientemente regolari proprio con polinomi.
Solo per questioni di completezza riportiamo qui l'enunciato del teorema relativo, nelle due forme in cui esso è solitamente presentato.
-
Formula di Taylor-Peano: Sia f una funzione
definita in un intervallo I = ]a,b[ e sia c
 I. Supponiamo che in I la funzione sia
derivabile n-1 volte e che in c esista
inoltre la derivata n-esima. Allora si ha, in I:
I. Supponiamo che in I la funzione sia
derivabile n-1 volte e che in c esista
inoltre la derivata n-esima. Allora si ha, in I:
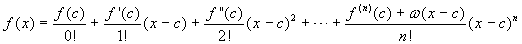 , ove
ω(x-c) è una funzione
infinitesima per x tendente a c.
, ove
ω(x-c) è una funzione
infinitesima per x tendente a c.
-
Formula di Taylor-Lagrange: Sia f una
funzione definita in un intervallo I = ]a,b[ e sia c
 I. Supponiamo che in I la funzione
sia derivabile n-1 volte, mentre esiste anche la
derivata n-esima in I\{c}. Allora per ogni
x di I\{c}
I. Supponiamo che in I la funzione
sia derivabile n-1 volte, mentre esiste anche la
derivata n-esima in I\{c}. Allora per ogni
x di I\{c} 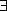 ξ tra x e c tale che:
ξ tra x e c tale che: 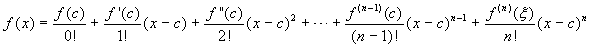 .
.
In sostanza il teorema consente di esprimere la funzione come la somma tra un polinomio e un termine, detto resto, che descrive di quanto la funzione si discosta dal polinomio. La formula di Taylor-Peano afferma in sostanza che il resto è "infinitesimo di ordine superiore" rispetto a (x-c)n e quindi consente di ottenere una approssimazione locale, cioè in un intorno di c, di una funzione con un polinomio. La formula di Taylor-Lagrange è più utile quando si vogliano fare stime accurate dell'errore che si commette approssimando la funzione con un polinomio, in un punto diverso da c.
In questa sede vogliamo occuparci proprio della precisazione del significato dell'aggettivo locale che caratterizza questa approssimazione, servendoci di opportune visualizzazioni grafiche.
Il problema nasce già con lo studio della derivata: se una funzione f(x) è derivabile in un punto c del suo dominio, allora, in un opportuno intorno del punto c stesso, la funzione può essere approssimata con la sua tangente, y = f'(c)(x-c) + f(c). Si noti che approssimare una funzione con la sua tangente significa approssimarla con un polinomio di primo grado. E' proprio utilizzando questa idea che si possono "tracciare" curve utilizzando un righello rettilineo. Si vedano, per esempio, le ben note costruzioni rappresentate nelle due figure qui sotto.

A volte si approssima una funzione addirittura con il suo valore in un punto (polinomio di grado zero): è per esempio la situazione comune quando si introduce l'integrale definito mediante la tecnica che si può dedurre dal grafico qui a lato, dove la funzione è approssimata con il valore costante che essa assume in una serie di punti (nel grafico abbiamo scelto i punti medi dei segmenti evidenziati, ma avremmo anche potuto fare diversamente).
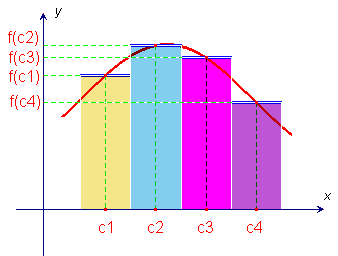
E' evidente che un'approssimazione mediante la tangente è, normalmente, "più accurata" in un intorno "più grande" che non l'approssimazione con il valore in un punto. La domanda che ci possiamo porre è allora la seguente: aumentando il grado del polinomio approssimante, possiamo ritenere che l'approssimazione diventi accurata in intervalli sempre più grandi, magari fino a coincidere con il dominio della funzione stessa? La risposta non è purtroppo sempre positiva, come vedremo con gli esempi delle pagine seguenti.
Prima di procedere diamo la seguente definizione di polinomio di Taylor di punto iniziale c, di ordine n, di una funzione f:
![]() .
.
E' naturale che la funzione in esame deve essere derivabile n volte in un intorno di c.