I numeri razionali
Per introdurre l'insieme dei razionali si usa un processo molto simile a quello seguito per introdurre gli interi.
Si consideri l’insieme Z×N\{0}. In esso si definisce la relazione (α,n)≈(β,m) se e solo se αm=βn. Non è difficile provare che si tratta di una relazione di equivalenza. Se, come fatto nel caso degli interi, rappresentiamo questo insieme in un piano cartesiano (in cui ci basteranno il primo e secondo quadrante), non è difficile provare che le classi di equivalenza sono costituite da tutti i punti che stanno sopra una stessa semiretta passante per l’origine (escluse le due semirette che stanno sull’asse delle ascisse).
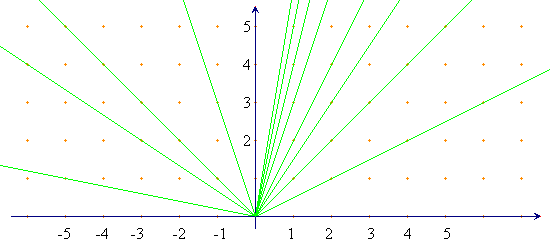
L’insieme quoziente Z×N\{0}/≈ si indica con Q e si chiama insieme dei numeri razionali; in esso è possibile introdurre un’operazione di somma e una di prodotto nel seguente modo: [(α,n)]+[(β,m)]=[(αm+βn,nm)], [(α,n)]·[(β,m)]=[(αβ,nm)]. Si prova poi che queste operazioni mantengono le proprietà di cui già godevano nell’insieme Z, e in più esiste il simmetrico rispetto alla moltiplicazione (detto usualmente reciproco) per tutti gli oggetti tranne zero.
Gli oggetti di
Z×N\{0}
si indicano di solito con la scrittura 
e si chiamano frazioni. Come è d’uso negli insiemi
quozienti si opera poi con un rappresentante delle varie classi
piuttosto che con le classi stesse, cioè in sostanza si
trattano le frazioni come se fossero
oggetti di
Z×N\{0}/≈.
Se si tiene conto di questo si vede subito che la relazione di
equivalenza sopra definita non è altro che quella, ben
nota, di equivalenza fra frazioni. Tenendo conto della
rappresentazione grafica sopra menzionata i numeri razionali
possono essere pensati come le pendenze (i coefficienti
angolari) delle rette passanti per l’origine.
É ora possibile introdurre in questo insieme un ordine con la seguente “definizione”: i numeri razionali, cioè le classi di equivalenza rappresentate da semirette passanti per l’origine, decrescono muovendosi in senso antiorario a partire dal semiasse positivo delle x fino al semiasse negativo delle x. La semiretta bisettrice del primo quadrante è il numero 1 (corrisponde alla classe[(α,α)], con α>0), cioè il neutro della moltiplicazione; il semiasse positivo delle y è il numero zero (corrisponde alla classe[(0,n)]), cioè il neutro dell’addizione; le semirette del primo quadrante sono i numeri positivi, quelle del secondo quadrante i negativi. Le frazioni del tipo (o meglio le classi di equivalenza [α,n]) con α divisibile per n, si comportano in tutto e per tutto come i vecchi numeri interi e possono essere identificate con essi. A questo punto possiamo pensare che Q sia un’estensione di Z.
Osservazioni
Il passaggio da Z a Q comporta
un notevole miglioramento in termini di qualità
(l’insieme dei razionali privati dello zero è un
gruppo commutativo anche rispetto alla operazione di prodotto)
tanto che Q ha una struttura algebrica nuova
detta corpo commutativo o
campo. Non si ha ancora invece alcun aumento in
termini di numero cardinale (cioè di quantità) che
rimane sempre 
0. La dimostrazione è molto semplice.
Per quanto riguarda la risoluzione delle equazioni è ora evidente che ogni equazione del tipo ax = b (con a non nullo), è risolubile.
L’insieme di numeri ora introdotto ha poi una nuova ed interessante proprietà relativamente all'ordine, resa evidente dalla rappresentazione grafica in termini di semirette passanti per l’origine: non è più possibile parlare di successivo di un numero. Infatti è immediato che tra due numeri razionali qualunque esiste sempre un altro numero razionale (anzi ne esistono infiniti…): se i due numeri sono a e b basta prendere, per esempio, (a+b)/2. Si dice che i numeri razionali sono densi in sé. Alla luce di questo è ancora più straordinario il fatto sopra menzionato che in termini di quantità questo insieme numerico abbia lo stesso cardinale dei naturali.
Perché non siamo ancora contenti?
Dal punto di vista della struttura algebrica e quindi della risolubilità delle equazioni (di primo grado) che abbiamo considerato, l'insieme dei razionali è perfettamente soddisfacente. Che motivo c'è allora di complicarsi ulteriormente la vita? La comprensione della "lacunosità" di questo insieme è, storicamente, legata alla scoperta del famoso teorema da parte della scuola di Pitagora: se un triangolo rettangolo ha i cateti uguali ad uno, quanto è lunga la sua ipotenusa?. Detto in altri termini: se ho un quadrato di lato 1, e quindi di area 1, quanto dovrà essere il lato di un quadrato che ha area doppia?
Usando il linguaggio delle equazioni questo problema è equivalente a quello di risolvere l'equazione x2 = 2. Questa equazione non può avere soluzioni in Q. Se infatti la frazione (ridotta ai minimi termini) m/n fosse una soluzione si dovrebbe avere m2=2n2. Ma questo non è possibile perché scomponendo in fattori primi m ed n avrei, in questa uguaglianza, un diverso numero di fattori uguali a 2 a destra e a sinistra dell'uguale.
E' molto importante segnalare che il problema in questione è squisitamente teorico: da un punto di vista pratico è possibile trovare una frazione che esprima l'ipotenusa del triangolo rettangolo isoscele di cateto 1 con un'approssimazione "grande quanto si vuole". Per esempio, come è ampiamente noto, 1414/1000, esprime la cercata ipotenusa con le prime tre cifre decimali esatte (il che è sufficiente per la quasi totalità delle applicazioni pratiche).
La risoluzione corretta di questo problema porta ad una nuova estensione dell'insieme di numeri, che conduce all'insieme dei reali. Questa estensione avviene con una tecnica completamente diversa da quelle finora utilizzate e produce un insieme sostanzialmente più ricco e complesso rispetto a quanto finora considerato.