I numeri interi
Per introdurre l'insieme degli interi possiamo utilizzare il seguente classico procedimento. Consideriamo l'insieme N×N e introduciamo in esso la relazione (n,m)≈(p,q) se n+q=m+p. Non è difficile verificare che si tratta di una relazione di equivalenza. L'insieme degli Interi, indicato con Z (dal tedesco Zahl, numero) è l'insieme quoziente N×N/≈.
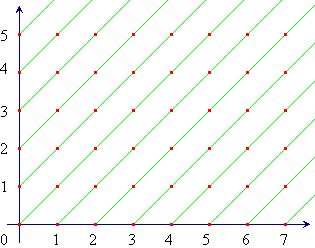
Per renderci visivamente conto di come questo insieme è costruito, consideriamo la rappresentazione di N×N nel piano cartesiano. Non è difficile rendersi conto che le classi di equivalenza rispetto alla relazione sopra indicata sono costituite da tutti e soli i punti che stanno su una stessa semiretta parallela alla bisettrice del primo e terzo quadrante.
Dovremo definire, in questo insieme di classi di equivalenza, le operazioni e l'ordine, e verificare che effettivamente il nuovo insieme è un gruppo (abeliano) rispetto all'operazione di somma.
Le definizioni di somma e prodotto si danno nel seguente modo (abbiamo indicato la classe di equivalenza di (n,m) con [(n,m)], seguendo l'uso):
-
[(n,m)]+[(p,q)] = [(n+p,m+q)]
-
[(n,m)]·[(p,q)] = [(np+mq,nq+mp)]
Non è difficile provare che si tratta di buone definizioni (cioè che il risultato delle operazioni dipende solo dalla classe e non dal rappresentante scelto) e che l'insieme che si ottiene è effettivamente un gruppo abeliano rispetto alla somma. Quello che qui ci interessa segnalare è che [(0,0)] è l'elemento neutro dell'addizione, [(1,0)] è l'elemento neutro della moltiplicazione e che [(m,n)] è l'opposto di [(n,m)].
É poi possibile introdurre un ordine in Z in modo che le classi [n,0] (cioè le semirette che stanno al di sotto della bisettrice) siano i numeri positivi e quelle [0,n] (cioè le semirette che stanno al di sopra della bisettrice) i negativi. A questo punto i numeri [n,0] si comportano esattamente come i vecchi numeri naturali e si indicano semplicemente con “n”, quelli [0,n] hanno la funzione di opposti dei precedenti e si indicano semplicemente con “–n”.
Nell’uso ci si dimentica quindi che i numeri interi sono classi di equivalenza nell’insieme N×N: si opera con essi esattamente come si faceva con i vecchi numeri naturali, anzi i numeri interi positivi si identificano con i naturali stessi. Questo modo di operare è giustificato proprio dal fatto che le operazioni eseguite sugli interi positivi si comportano esattamente come quelle sui naturali e che l’ordine sugli interi positivi riproduce esattamente quello sui naturali. Si usa dire che l’insieme degli interi è un’estensione di quello dei naturali.
É da segnalare che spesso i numeri interi sono definiti (o almeno pensati) come una coppia costituita da un numero naturale e un segno. Questo modo di procedere non è corretto perché porterebbe a considerare i due numeri “+0” e “–0” come diversi e anche se l’inconveniente potrebbe essere superato con qualche artificio si otterrebbe una teoria poco lineare ed elegante.
Osservazioni
Il passaggio dall’insieme dei naturali a quello degli
interi produce un notevole salto in termini di qualità
(l’insieme degli interi è un gruppo commutativo
rispetto alla somma, mentre conserva quasi le stesse
caratteristiche dei naturali nei riguardi del prodotto), ma non
produce nessun aumento in termini di cardinalità
(cioè di quantità), in quanto è immediato
provare che gli interi e i naturali sono equipotenti: il
cardinale rimane ancora 
0. La prova che la cardinalità non
è cambiata si può fare semplicemente, costruendo
la corrispondenza biunivoca tra i naturali e gli interi che
associa ad ogni naturale pari un intero positivo e ad ogni
naturale dispari un intero negativo.
La rappresentazione grafica che abbiamo sopra riportato rende anche evidente che gli interi sono simili ai naturali anche per un altro aspetto: esattamente come i naturali gli interi sono “naturalmente” distanti uno dall’altro, cioè tra un intero e il successivo non esiste alcun altro intero. Anche se l'insieme degli interi non ha un minimo, sostanzialmente il tipo di ordine è rimasto lo stesso.
Per quanto riguarda la risolubilità delle equazioni è chiaro che, ora, una qualunque equazione del tipo x + a = b sarà risolubile.
Il secondo passo nell'ampliamento del nostro insieme numerico costituisce nel costruire un insieme in cui anche il prodotto goda della proprietà dell'esistenza del simmetrico: si otterrà l'insieme dei razionali.