Questo limite gioca un'importanza fondamentale in matematica. Il suo calcolo procede in diverse tappe:
- Si prova che il limite esiste.
- Si prova che il limite è compreso tra 2 e 3.
- Si prova che il limite è un numero trascendente.
A questo punto si introduce per il valore di questo limite un simbolo speciale, la lettera "e", che prende il nome di numero di Nepero, dal matematico scozzese John Napier (anche se Napier non lo utilizzò mai). La prova della trascendenza di questo numero è dovuta a Hermite (1873), mentre già Eulero (1737) aveva dimostrato che era irrazionale. É interessante osservare che, assieme a π, questo è uno dei pochi numeri trascendenti usati nella pratica comune e che hanno un simbolo speciale. Come curiosità segnaliamo che mentre è noto che eπ è un numero trascendente, non si sa ancora se πe sia razionale o irrazionale.
Ovviamente la dimostrazione del punto 3 è abbastanza
complessa ed esula dagli scopi di questa monografia; per la
dimostrazione dei punti 1 e 2, conviene considerare prima il
. La dimostrazione dell'esistenza del
limite si fa provando che la successione 
è crescente. Si ha: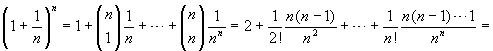 
. Se in questa somma si sostituisce
n+1 al posto di n, la somma cresce, inoltre
viene aggiunto un termine positivo alla fine: la successione
è dunque crescente.
Lo stesso calcolo prova poi che valgono le disuguaglianze e uguaglianze seguenti:
. Questo basta
per concludere. A questo punto è facile estendere il
risultato anche alla funzione 
.
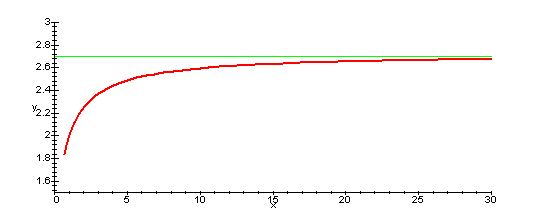
Per rendere chiaro il significato dei calcoli proposti, si
può esaminare il grafico della funzione . In verde è rappresentata la retta y=e,
verso cui la funzione tende asintoticamente.
