Qualche esempio conclusivo
Esempio1
Tracciare il grafico di ![]() . Procediamo per gradi tracciando
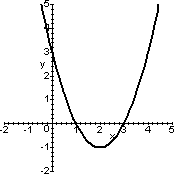
prima il grafico di x2-4x+3, o direttamente
come parabola o osservando che
x2-4x+3=(x-2)2-1, poi quello di
|x2-4x+3|, di
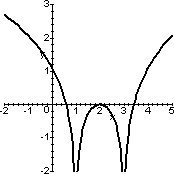
ln|x2-4x+3|, di
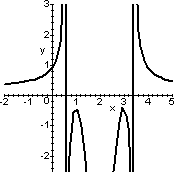
1/ln|x2-4x+3| ed infine quello richiesto. I
grafici sono proposti qui sotto.
. Procediamo per gradi tracciando
prima il grafico di x2-4x+3, o direttamente
come parabola o osservando che
x2-4x+3=(x-2)2-1, poi quello di
|x2-4x+3|, di
ln|x2-4x+3|, di
1/ln|x2-4x+3| ed infine quello richiesto. I
grafici sono proposti qui sotto.
|
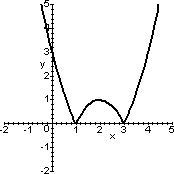
|
|
|

|
Esempio 2
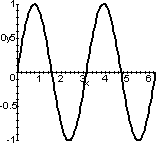
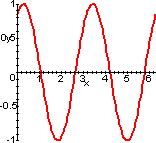
Tracciare f(x)=sin(2x+1). Si può osservare che sin(2x+1)=sin(2(x+1/2)). Si può dunque partire dalla funzione sin(x), costruire poi sin(2x) (cambiamento di scala sull'asse x) e infine sin(2x+1) (traslazione).

|
|
|
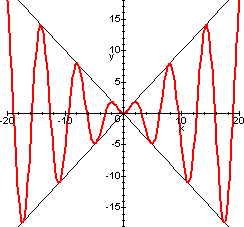
Esempio 3
Tracciare il grafico di f(x)=xsinx. In questo caso non si possono usare le tecniche proposte, tranne nei tratti ove il seno è crescente e x è positiva (prodotto di funzioni crescenti e positive) (o analogamente il seno è decrescente e x negativa). Si può però osservare che -1≤sinx≤1 e quindi -x≤xsinx≤x. Questo significa che la funzione f(x) tocca la funzione x oppure -x nei punti dove il seno vale 1 o -1. Questo non ci permette di stimare dove saranno i massimi o i minimi di f(x) (sicuramente un po' dopo dei punti dove il seno vale 1 o -1), ma comunque ci consente di abbozzare il grafico che avrà un andamento del tipo di quello tracciato qui sotto.