Cenno alle disequazioni in due incognite
Se per le disequazioni in un'incognita reale la tecnica grafica era un optional, per le disequazioni in due incognite diventa praticamente obbligatoria: non esistono metodi analitici semplici per scrivere le soluzioni delle disequazioni in due incognite, per cui di solito l'insieme di soluzioni viene graficamente rappresentato nel piano di Gauss. In questa breve introduzione tratteremo solo le disequazioni di primo e secondo grado e semplici sistemi.
Il principio generale
Considerata una funzione f : D (
R2) →
R, z = f(x,y), l'insieme
dei punti dove f(x,y) = 0, cioè l'insieme
degli zeri della funzione, è un sottoinsieme del piano
cartesiano Oxy, dove si rappresenta il dominio
D della funzione f. Geometricamente si
può pensare come l'insieme ottenuto
dall'intersezione del grafico della funzione f con
il piano Oxy. Nei casi che a noi interesseranno questo
insieme è una retta (se la funzione f è
un polinomio di primo grado in due incognite:
f(x,y)=ax+by+c), oppure una conica (se la funzione
è un polinomio di secondo grado in due incognite:
f(x,y)=ax2+bxy+cy2+dx+ey+f).
Le disequazioni che considereremo saranno sempre del tipo f(x,y)>0 (oppure <0, oppure ≥0, oppure ≤0). Poiché la retta o la conica divide il piano in due (tre per il caso dell'iperbole, ma come vedremo potremo sempre ragionare come se fossero due) regioni disgiunte, la disequazione sarà sempre verificata in una delle due e non verificata nell'altra: basterà solo provare con un punto interno ad una delle regioni, come vedremo negli esempi.
Disequazioni di primo grado
Esempio 1. Risolvere la disequazione 2x+3y-6>0.
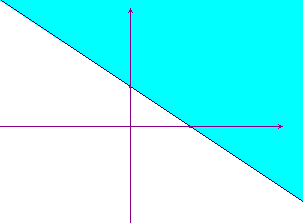
Rappresentata la retta 2x+3y-6=0, se si prova a sostituire nella disequazione le coordinate dell'origine degli assi si ottiene -6>0 che è falsa: l'insieme delle soluzioni è allora l'altro semipiano, rappresentato in azzurro nel grafico qui sotto.
Esempio 2. Risolvere la disequazione x - 2y + 1 ≤ 0.
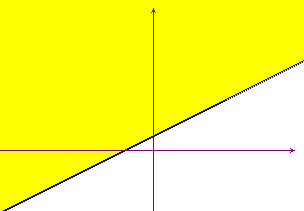
Rappresentata la retta x - 2y + 1 = 0, se si prova a sostituire nella disequazione le coordinate dell'origine degli assi si trova 1 ≤ 0, che è falsa: l'insieme di soluzioni è allora l'altro semipiano, rappresentato in giallo nel grafico qui sotto. Questa volta anche il bordo del semipiano, cioè la retta, fa parte dell'insieme delle soluzioni.
Disequazioni di secondo grado
Esempio 1. Risolvere la disequazione
x2 - 3y2 + 4x - 6y - 4 < 0.
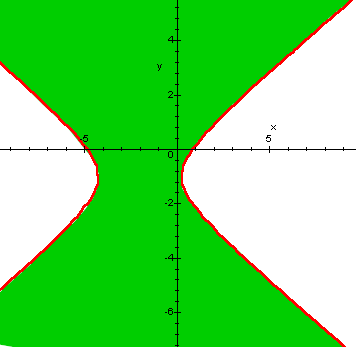
Rappresentata l'iperbole x2 - 3y2 + 4x - 6y - 4 = 0, se si sostituiscono nella disequazione le coordinate dell'origine si ottiene -4<0 che è vera: la disequazione è allora verificata in tutta la parte di piano individuata dall'iperbole e a cui appartiene l'origine (colorata di verde nel grafico qui sotto). L'iperbole in realtà divide il piano in tre regioni distinte, ma se si tiene conto di come è originata l'iperbole si possono considerare le due "interne" (quelle non colorate in questo grafico) come un'unica regione che "si salda" all'infinito.
Esempio 2. Risolvere la disequazione
8x2 - 4xy + 5y2 - 144 <
0.
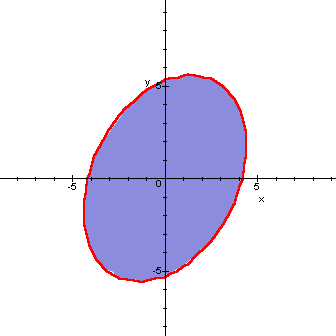
Sistemi di disequazioni o di equazioni e disequazioni
Come per il caso di un'incognita si potranno considerare sistemi di disequazioni: basterà considerare l'intersezione tra gli insiemi soluzioni delle varie disequazioni.
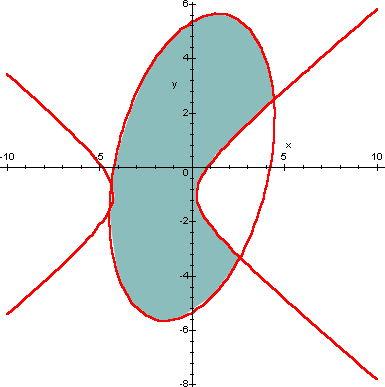
Il sistema, per esempio, tra le due disequazioni considerate sopra ha come insieme di soluzioni la regione colorata nel grafico qui sotto.
Sono molto importanti nelle applicazioni anche i sistemi tra equazioni e disequazioni in due incognite, che si risolveranno sempre intersecando l'insieme soluzione della equazione (una curva nei casi che ci interessano) e l'insieme soluzione della disequazione (un opportuno sottoinsieme del piano).
Esempio. Risolvere il sistema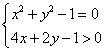 
L'insieme soluzione è l'arco di circonferenza rappresentato in verde nel grafico qui sotto. Esso è stato ottenuto intersecando la circonferenza (insieme delle soluzioni della equazione di secondo grado) e il semipiano colorato in giallo (insieme delle soluzioni della disequazione di primo grado).
Sopragrafici e sottografici
Se consideriamo una funzione g : A (R) →
R, y = g(x), possiamo sempre
considerare il suo grafico come l'insieme degli zeri della
funzione f : D=A×R
( R2)
→ R, z = f(x,y)=y -
g(x). L'insieme soluzione della disequazione
f(x,y)>0, ovvero y>g(x), è detto
sopragrafico della funzione g.
L'insieme soluzione della disequazione f(x,y)<0,
ovvero y<g(x), è detto
sottografico della funzione g. Questi
concetti hanno importanza, per esempio, nella definizione di
funzione convessa: una funzione si dice
convessa se il suo sopragrafico è un insieme convesso (un
insieme che contiene tutti i segmenti aventi estremi
nell'insieme stesso).
La rappresentazione di questi insiemi è immediata e solo per completezza forniamo un esempio.
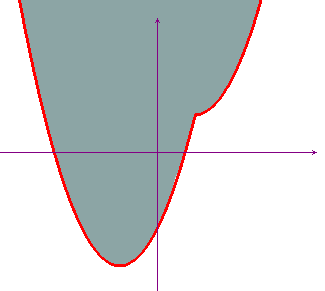
Esempio. Trovare il sopragrafico della funzione f(x)=x2-2|x-1|. Il risultato è la regione piana colorata nella figura qui sotto. Si noti come questa regione non sia convessa, per cui la funzione data non è convessa.
