Ma che significa?
Equazioni e disequazioni
Risolvere una disequazione, nell'incognita reale x, significa risolvere il seguente problema:
Dato un insieme D (sottoinsieme di R),
e due funzioni 
, trovare
l'insieme S, detto insieme
delle soluzioni, in cui si ha
f(x)≤g(x) (oppure
f(x)≥g(x), f(x)< g(x), f(x)>
g(x)).
Risolvere un'equazione significa, nelle stesse ipotesi, trovare l'insieme S in cui f(x) = g(x).
Se l'equazione o la disequazione è in due incognite l'insieme D sarà un sottoinsieme di R2 e le funzioni f e g saranno funzioni di due variabili (naturalmente sempre a valori in R).
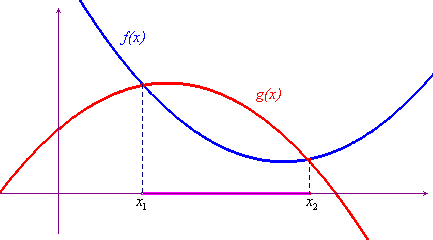
Nel caso di un'incognita, di cui prevalentemente ci occuperemo, considerati i grafici delle due funzioni f e g, si tratterà, per le disequazioni, di determinare l'insieme dei punti dell'asse delle ascisse in cui il grafico di f sta "al di sotto" di quello di g (oppure "al di sopra" a seconda dei casi), mentre per le equazioni si dovrà trovare l'insieme dei punti dell'asse delle ascisse in corrispondenza dei quali i due grafici si intersecano.
Nel grafico qui sotto, per esempio, l'intervallo dei punti compresi tra x1 e x2 (esclusi gli estremi) è l'insieme delle soluzioni della disequazione f(x)<g(x). Lo stesso grafico fornisce immediatamente le soluzioni della disequazione che si ottiene cambiando il verso (f(x)>g(x)), o della eventuale equazione f(x)=g(x).
Se la funzione g è identicamente nulla l'equazione, o disequazione, si dice ridotta in forma normale: f(x)=0, f(x)≤0, f(x)≥0, ecc. In questo caso si deve confrontare il grafico della funzione f con l'asse delle x, cioè, come vedremo, si deve trovare il segno della funzione f. É chiaro che si può sempre passare da una forma all'altra con semplici passaggi algebrici. Dal punto di vista tecnico a volte una forma è più agevole da trattare dell'altra, come vedremo con degli esempi, ma non esistono regole generali.
Nel grafico qui sotto l'unione degli intervalli di estremi x1- x2 ed x3 - x4, rispettivamente, è l'insieme delle soluzioni della disequazione f(x)>0.
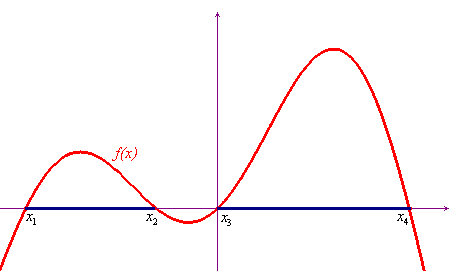
Nei casi pratici, di norma, l'insieme D non è dato e si conviene che esso sia il dominio naturale comune alle due funzioni f e g, che si può chiamare dominio della disequazione (o della equazione).
La ricerca di questo dominio naturale deve essere fatta prima di
risolvere la disequazione e
prima di ogni possibile semplificazione.
Chiariamo questo fatto con un esempio. Sia data la disequazione
. Il dominio naturale è
R\{0} e la disequazione risulta verificata per
tutti gli x compresi tra -1 e 1 ma diversi da
zero. Se si "semplifica" la frazione 1/x si
ottiene una disequazione completamente diversa che ha come
insieme delle soluzioni tutti gli x compresi tra -1 e
1, compreso lo zero.
Segno delle funzioni
Strettamente connesso con il problema di risolvere una disequazione è quello di determinare il segno di una funzione (a valori reali). Data la funzione f si deve:
- Trovarne il dominio naturale D (se già non è assegnato il dominio nel testo).
- Trovare il sottoinsieme di D dove f(x)=0.
- Trovare il sottoinsieme di D dove f(x)>0.
- Trovare il sottoinsieme di D dove f(x)<0.
La determinazione del segno prevede quindi, dopo aver trovato il dominio, la risoluzione di un'equazione e di due disequazioni. Dal punto di vista tecnico, come vedremo, in molti casi la determinazione del dominio e dei punti dove f(x)>0 consente di determinare agevolmente anche l'insieme dei punti dove f(x)=0 e quello dove f(x)<0. La situazione non è comunque sempre così semplice e conviene prestare la massima attenzione.
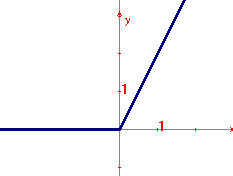
Chiariamo anche questo fatto con un esempio. Si consideri la funzione f(x)=x+|x|. Essa ha come dominio naturale R, è positiva per x>0, si annulla per x≤0, non è mai negativa. La cosa risulta evidente se si considera il grafico rappresentato qui sotto, e si può anche ricavare con metodi algebrici, come vedremo.
In molte applicazioni è importante la funzione
signum, così definita: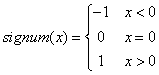 
.
La useremo spesso nel trattare le disequazioni, anche se in un
modo un po' improprio. Precisamente, data una funzione
f, con la scrittura signum(f), o più
brevemente sgn(f) intenderemo indicare il segno di una
funzione, nel senso sopra indicato.