www.batmath.it

Il famigerato "studio di funzione"

"Studiare" una funzione (reale di variabile reale) significa determinarne le caratteristiche essenziali fino a tracciare un grafico indicativo. Si tratta di uno dei cavalli di battaglia più famosi nei temi sia dell'esame di stato di scuola media superiore, che dei primi esami di analisi all'università. Ora questo problema ha perso gran parte del suo fascino (?!) con l'avvento dei calcolatori che riescono a darci informazioni spesso adeguate in frazioni di secondo. Non sempre però le informazioni desumibili da un grafico al calcolatore sono sufficienti per gli scopi prefissati e, in ogni caso, questo argomento può essere considerato un momento di verifica conclusivo e complessivo delle abilità raggiunte nello studio dell'analisi. Per questo, pur senza insistere su esercizi tecnicamente complessi, lo studio di funzione continua a rimanere fondamentale nelle prove e nei test e merita una considerazione speciale in una monografia sul calcolo differenziale.

Ci interesseranno in maniera quasi esclusiva le funzioni costruite a partire da funzioni elementari. Per esse i punti fondamentali per concludere un completo studio possono essere elencati come segue:

1. Determinazione del dominio naturale. Per le funzioni indicate si intende con dominio naturale il più ampio sottoinsieme di R dove le operazioni da eseguire per calcolare i valori della funzione hanno senso.
2. Determinazione del segno della funzione.
3. Determinazione degli eventuali punti di discontinuità.
4. Determinazione dei cosiddetti limiti notevoli. Le funzioni indicate sono di solito continue in quasi tutti i punti del loro dominio; ha quindi interesse verificare l'andamento delle funzioni in un intorno dei punti di non continuità o in un intorno dei punti di accumulazione del dominio che non stanno del dominio: sono questi i limiti notevoli.
5. Determinazione degli eventuali asintoti.
6. Calcolo della derivata prima, determinazione degli eventuali punti di non derivabilità, determinazione degli intervalli di crescenza e decrescenza, determinazione degli eventuali estremi relativi e assoluti.
7. Calcolo della derivata seconda, determinazione degli eventuali punti in cui tale derivata non esiste, determinazione degli intervalli di convessità o concavità, determinazione degli eventuali flessi.
8. Tracciamento di un grafico indicativo di tutte le informazioni ottenute.

A questi punti vanno aggiunte alcune altre considerazioni, come si può vedere nella pagina delle finezze. É da segnalare che, spesso, non tutti i punti indicati sono tecnicamente agevoli da trattare: quelli assolutamente irrinunciabili sono i numeri 1, 4, 6. 

Da un punto di vista pratico è conveniente riportare subito i risultati che si vanno via via determinando in un grafico cartesiano, senza aspettare di avere concluso tutti i punti: quasi sempre è possibile rendersi conto più facilmente di eventuali errori, a causa delle incompatibilità tra i diversi risultati ottenuti.

Avendo a disposizione una calcolatrice grafica (cosa che auspichiamo diventi possibile entro breve anche agli esami di stato!), è utile fare una verifica sommaria della validità dei risultati ottenuti, prestando tuttavia la massima attenzione alle ovvie limitazioni a cui è sottoposto un simile strumento. Sarebbe, a nostro avviso, molto meglio abituare lo studente a valutare questo tipo di limitazioni e a sapersi comportare di conseguenza, piuttosto che proibire l'uso dei moderni strumenti di calcolo.

Un esempio chiarirà il metodo da seguire.

Esempio. Studiare la funzione .

1. Il dominio della funzione si trova risolvendo la disequazione 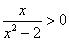. Si trova facilmente .
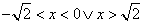2. Per trovare il segno basta risolvere la disequazione 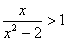. Si trova facilmente che la funzione è positiva per 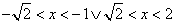, negativa per 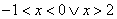, mentre si annulla per . 
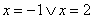3. La funzione è continua in tutti i punti del dominio, in quanto funzione elementare.
4. Per i limiti notevoli, che in questo caso si riducono a quelli sui punti di accumulazione del dominio che non stanno nel dominio, si ha facilmente: , , , .
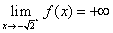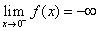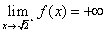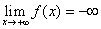5. Dai risultati del punto 4 si ottiene che le rette 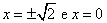sono asintoti verticali. Per gli asintoti obliqui si deve calcolare il 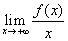. Si può usare la regola di l'Hôpital per concludere che questo limite è zero, per cui non ci sono asintoti obliqui.
6. Si trova facilmente . Se ne deduce che la funzione, nel dominio, è sempre derivabile con derivata negativa, ovvero è decrescente.
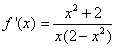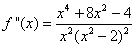7. Si trova facilmente . Se ne deduce che la funzione ha un flesso nel punto di ascissa 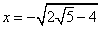 , mentre è convessa prima di questo valore e dopo il valore . 
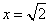8. I risultati precedenti sono riassunti nel seguente grafico: 

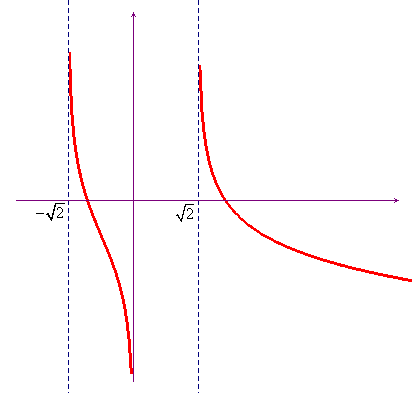
Oltre che sul grafico cartesiano è opportuno riportare via via anche su un grafico del tipo +/- usato per le disequazioni i risultati relativi al dominio e al segno della funzione e delle sue derivate. Nell'esempio appena considerato il grafico in questione ha il seguente aspetto, con evidente significato dei simboli:

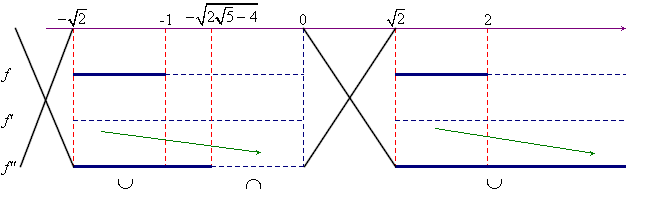
Spesso, nei testi classici di analisi, vengono presentati esercizi su questo argomento divisi per categorie: funzioni razionali intere, funzioni fratte, funzioni trigonometriche, ecc. Riteniamo inutile e dannosa una tale distinzione che ingenera nello studente la falsa convinzione che ogni categoria richieda metodi suoi propri, cosa assolutamente falsa: è per questo che abbiamo proposto come primo esempio una funzione logaritmica.

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 01/10/2002 - ultimo aggiornamento il 01/09/2003