www.batmath.it
Derivate successive nella ricerca degli estremi - dimostrazione
Se la funzione f definita in I=]a,b[ è
derivabile n volte in I e si ha
f'(c)=f''(c)=...=f(n-1)(c)=0,
mentre f(n)(c)≠0, allora:
- se n è pari la funzione ha in c un massimo o un minimo relativo a seconda che f(n)(c)<0 oppure f(n)(c)>0;
- se n è dispari la funzione è crescente o decrescente in c a seconda che f(n)(c)>0 oppure f(n)(c)<0.
La dimostrazione si basa sull'uso della formula di Taylor, certamente applicabile nel nostro
caso e che, tenendo conto dell'annullarsi delle derivate
come nell'enunciato, si riduce a: ![]() . Poiché
. Poiché ![]() , per il teorema
della permanenza
del segno
, per il teorema
della permanenza
del segno ![]() ha lo stesso segno di
ha lo stesso segno di
![]() in un intorno di c. Tenendo conto
che n è l'esponente di x-c si
deduce che, in quest'intorno,
in un intorno di c. Tenendo conto
che n è l'esponente di x-c si
deduce che, in quest'intorno,
-
se n pari
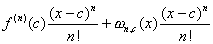 ha lo stesso
segno segno di
ha lo stesso
segno segno di 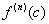 , per cui f(x)
è sempre maggiore o minore di f(c), ovvero la
f ha un minimo o un massimo;
, per cui f(x)
è sempre maggiore o minore di f(c), ovvero la
f ha un minimo o un massimo;
-
se n è dispari
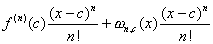 cambia di segno passando dalla sinistra alla destra
del punto c, ovvero il punto non è né
di massimo né di minimo e la funzione è
crescente o decrescente a seconda del segno di
cambia di segno passando dalla sinistra alla destra
del punto c, ovvero il punto non è né
di massimo né di minimo e la funzione è
crescente o decrescente a seconda del segno di 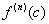 .
.
copyright 2000 et seq. maddalena falanga & luciano battaia
pagina pubblicata il 01/10/2002 - ultimo aggiornamento il
01/09/2003