Esercizi risolti - 2
Esercizio 11. Provare, usando
esclusivamente il significato combinatorio dei simboli, la
seguente uguaglianza:
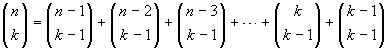 .
.
Si tratta di fare una dimostrazione che non utilizzi il valore
numerico dei simboli o altre proprietà dei coefficienti
binomiali, ma solo il loro significato insiemistico. Il primo
membro rappresenta il numero dei sottoinsiemi a
k
elementi di un insieme di
n elementi. Per verificare
l'uguaglianza cerchiamo di contare questi sottoinsiemi in un
altro modo. Numeriamo gli elementi dell'insieme da 1 a
n, e ragioniamo, per semplicità, su un esempio
concreto, ponendo
n=7 e
k=3. Per contare i
sottoinsiemi di 3 elementi dall'insieme di 7, posso
cominciare a contare quelli che hanno come minimo elemento 1;
essi sono in numero di
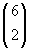
, in quanto, fissato
l'1, devo scegliere i restanti due elementi della terna tra
i residui 6 elementi dell'insieme:
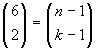
.
Poi conto quelli che cominciano con 2, che saranno, per lo
stesso motivo di prima,
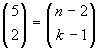
. Di seguito
conterò quelli che cominciamo con 3, 4, 5 che saranno,
rispettivamente,
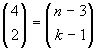
,
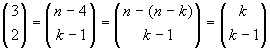
,
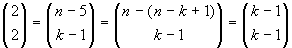
. Una
generalizzazione immediata porta alla formula richiesta.
Esercizio 12. Calcolare 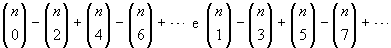 .
.
Si può procedere calcolando
(1+
i)
n in due modi diversi.
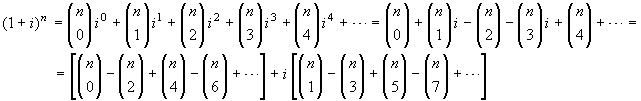 .
.
D'altro canto 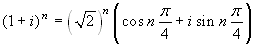 . I valori
richiesti si trovano ora per confronto.
. I valori
richiesti si trovano ora per confronto.
Esercizio 13. Provare la formula 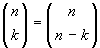 , esclusivamente in termini di sottoinsiemi.
, esclusivamente in termini di sottoinsiemi.
Il primo membro rappresenta i sottoinsiemi con k
elementi di un insieme con n elementi, il secondo
membro i sottoinsiemi con n-k elementi. E' chiaro
che se un sottoinsieme ha k elementi, il suo
complementare ne ha n-k. La formula esprime allora
semplicemente il fatto che ogni sottoinsieme di un insieme ha un
unico complementare.
Esercizio 14. Provare
l'uguaglianza 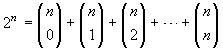 contando in due
modi diversi i numeri di n cifre in binario.
contando in due
modi diversi i numeri di n cifre in binario.
I numeri di
n cifre sono le disposizioni con
ripetizione di 2 simboli (0 ed 1) a
n a
n, e
pertanto sono 2
n. Contiamo ora questi numeri
in altro modo. Iniziamo con quelli che non contengono nessun 1:
ce n'è uno solo,
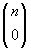
, quello che ha
tutti 0. I numeri che contengono un solo 1 sono
n,
ovvero
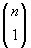
, corrispondenti alle possibili scelte
dove mettere il numero 1 su
n posizioni. I numeri con
due 1 sono
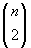
, corrispondenti alle possibili scelte
delle due posizioni, su
n, in cui mettere gli 1. La
conclusione è ora banale.
Esercizio 15. Dimostrare che 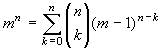 .
.
La dimostrazione è quasi immediata usando la formula del
binomio, dopo aver osservato che
m = (1+
m-1).
Vogliamo però procedere in un altro modo per mettere in
evidenza il significato combinatorio dei simboli. Si può
fare un confronto con la soluzione dell'esercizio 14.
Contiamo i numeri di
n cifre in un sistema con
m simboli: {
s1,
s2, ...,
sm}. Il primo
membro è il conteggio diretto mediante le disposizioni
con ripetizione degli
m simboli. Contiamo ora i numeri
che non contengono il simbolo
s1: sono tanti
quanti i numeri che contengono solo i restanti simboli, ovvero
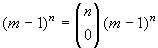
. La quantità di numeri che
contengono 1 volta il simbolo
s1 si ottiene
contando gli
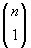
posti dove si
può mettere
s1 e moltiplicando per
(
m-1)
n-1 che sono i modi di
disporre i restanti
m-1 simboli. Analogamente la
quantità di numeri che contengono 2 volte il simbolo
s1 si otterrà moltiplicando
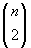
per (
m-1)
n-2 e
così via.
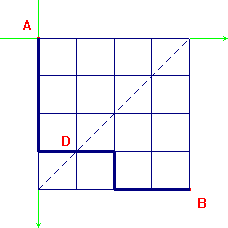 Esercizio
16. Considerata una griglia quadrata di lato n
come in figura, si chiede di contare in due modi diversi i
cammini di minima lunghezza per andare dall'estremo sinistro
in alto (A) all'estremo destro in basso (B).
Esercizio
16. Considerata una griglia quadrata di lato n
come in figura, si chiede di contare in due modi diversi i
cammini di minima lunghezza per andare dall'estremo sinistro
in alto (A) all'estremo destro in basso (B).
Un cammino qualunque di minima lunghezza da A a B ha lunghezza
2
n e consta di
n passi nella direzione
x e di
n passi nella direzione
y. Per
caratterizzare i percorsi devo decidere quali passi devo fare
nella direzione
x (oppure, il che è lo stesso,
nella direzione
y), cioè devo scegliere
n elementi su un totale di 2
n: il risultato
è
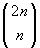
. D'altro canto ogni cammino deve
passare per un punto D della diagonale e i cammini da A a D e da
D a B hanno lunghezza
n. Se D ha coordinate
(
k,n-k), ripetendo il ragionamento di sopra si vede che
i cammini da A a D sono
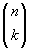
, come quelli da D a
B. I cammini da A a B che passano per D saranno allora
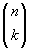
.
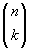
. Sommando tutte le
possibilità si ottiene la nota formula
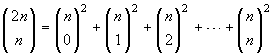
.
Esercizio 17. Dimostrare la formula
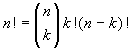 , ragionando sulle permutazioni di un
insieme di n oggetti.
, ragionando sulle permutazioni di un
insieme di n oggetti.
Il primo membro rappresenta le permutazioni indicate. Si tratta
di provare a contarle in un altro modo. Si possono scegliere
k degli
n oggetti, in
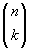
modi diversi, e poi fare le
k! loro permutazioni e le
(
n-k)! permutazioni dei rimanenti. In questo modo si
è provata la formula richiesta. Si noti come questo
ragionamento costituisca una dimostrazione alternativa della
nota formula riguardante i coefficienti binomiali.
Esercizio 18. Verificare, per
induzione, che 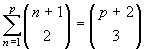 .
.
*) L'uguaglianza è vera per
p=1, in quanto
si riduce a
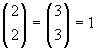
.
**) Supposta vera l'uguaglianza per p,
dimostriamola per p+1. Si tratta solo di eseguire i
calcoli, ottenendo: 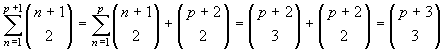 , l'ultima
uguaglianza essendo giustificata dalla formula di Stifel.
, l'ultima
uguaglianza essendo giustificata dalla formula di Stifel.
Esercizio 19. Dimostrare, ragionando
esclusivamente sui sottoinsiemi di un insieme, la formula 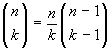 .
.
Il primo membro rappresenta il numero dei sottoinsiemi con
k elementi di un insieme, diciamolo A, di
n
elementi. Vediamo di contare questi sottoinsiemi in modo
diverso. Indicati con
a1,
a2, ...,
an, gli
elementi di A, consideriamo l'insieme B che si ottiene
escludendo
an e costruiamo i suoi
sottoinsiemi di
k-1 elementi. Essi sono in numero di
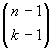
. Se ad ognuno di questi aggiungiamo
an otteniamo
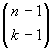
sottoinsiemi a
k elementi di A, che sono tutti quelli
che contengono
an. Vediamo ora di ottenere
anche gli altri. Ad ognuno dei sottoinsiemi di B aggiungiamo uno
degli elementi di B che non gli appartengono, e che sono in
numero di
n-k. Otteniamo
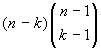
insiemi, sottoinsiemi di A, con
k elementi. Ciascun
sottoinsieme è però ripetuto in questo modo
k volte. Per rendercene conto consideriamo, per
esempio, l'insieme {
a1,
a2, ...,
ak-1}.
Aggiungendoci
ak otteniamo l'insieme C =
{
a1,
a2, ...,
ak-1, ak}. C si ottiene
però anche da {
a1,
a2, ...,
ak-2,
ak}, aggiungendo
ak-1, e così via. Ci sono
chiaramente
k modi di ottenere C. Dunque i sottoinsiemi
di A con
k elementi, che non contengono
an,
sono in numero di
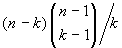
. Il totale
è allora:
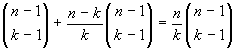
, con il che
l'uguaglianza è provata. Si noti che
l'uguaglianza poteva essere provata in modo immediato usando
la nota formula per i coefficienti binomiali, ma la
dimostrazione che abbiamo fornito rende più chiaro il
significato insiemistico dei coefficienti stessi.
Esercizio 20. Risolvere
l'equazione 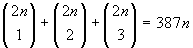 .
.
Applicando anche la formula di Stifel si ha
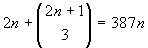
. Basta ora applicare la formula per i coefficienti
binomiali per trovare
n=17.
copyright 2000 et seq. maddalena falanga & luciano battaia
pagina pubblicata il 07/05/2004 - ultimo aggiornamento il
30/08/2004
![]() .
.
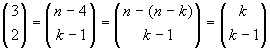 ,
, 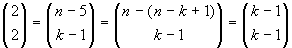 . Una
generalizzazione immediata porta alla formula richiesta.
. Una
generalizzazione immediata porta alla formula richiesta.
![]() .
.
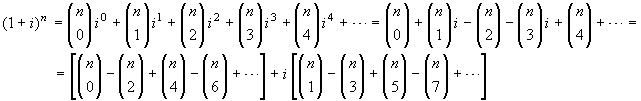 .
.
![]() . I valori
richiesti si trovano ora per confronto.
. I valori
richiesti si trovano ora per confronto.
![]() , esclusivamente in termini di sottoinsiemi.
, esclusivamente in termini di sottoinsiemi.
![]() contando in due
modi diversi i numeri di n cifre in binario.
contando in due
modi diversi i numeri di n cifre in binario.
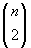 , corrispondenti alle possibili scelte
delle due posizioni, su n, in cui mettere gli 1. La
conclusione è ora banale.
, corrispondenti alle possibili scelte
delle due posizioni, su n, in cui mettere gli 1. La
conclusione è ora banale.
![]() .
.
 Esercizio
16. Considerata una griglia quadrata di lato n
come in figura, si chiede di contare in due modi diversi i
cammini di minima lunghezza per andare dall'estremo sinistro
in alto (A) all'estremo destro in basso (B).
Esercizio
16. Considerata una griglia quadrata di lato n
come in figura, si chiede di contare in due modi diversi i
cammini di minima lunghezza per andare dall'estremo sinistro
in alto (A) all'estremo destro in basso (B).
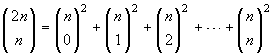 .
.
![]() , ragionando sulle permutazioni di un
insieme di n oggetti.
, ragionando sulle permutazioni di un
insieme di n oggetti.
![]() .
.
![]() , l'ultima
uguaglianza essendo giustificata dalla formula di Stifel.
, l'ultima
uguaglianza essendo giustificata dalla formula di Stifel.
![]() .
.
![]() .
.