Esercizi risolti - 1
Esercizio 1. Quanti sono i numeri di 6
cifre con almeno una cifra dispari? E quelli con almeno una
cifra pari?
Intanto calcoliamo quanti sono i numeri di sei cifre; tenendo
conto che non possono cominciare per 0, sono
9·10·10·10·10·10 = 900000.
Posso poi calcolare i numeri che hanno solo cifre pari; in
questo caso ho 4 scelte per il primo posto e 5 per ciascuno
degli altri 5, quindi 4·55 = 12500. Invece i
numeri che hanno solo cifre dispari sono 56 (lo zero
non è dispari), cioè 15625. Si ottiene
900000-12500=887500 per la prima richiesta, 884375 per la
seconda.
Esercizio 2. Quante sono le soluzioni
naturali dell'equazione x+y+z =
33, con le condizioni x≥4 e y≥7?
Se non ci fossero le condizioni si tratterebbe di trovare le
combinazioni con ripetizione di 3 oggetti di classe 33,
ottenendo Cr3,33 =
C3+33-1,33 = C35,33 =
595. Le limitazioni poste implicano che ci sono 22 oggetti da
distribuire: è esattamente come risolvere
l'equazione x+y+z = 22. Ci
sono C24,22 = 276 possibilità.
(*)Esercizio 3. Data una funzione a
valori reali
f(x1,x2,...,xn) di
n variabili reali, quante derivate parziali di ordine
k ammette, nell'ipotesi che si possa scambiare
l'ordine di derivazione?
Si tratta delle combinazioni con ripetizione di n
oggetti (posso derivare rispetto ad una qualunque delle
variabili) di classe k (in totale devo derivare
k volte):
Crn,k.
Esercizio 4. Si vogliono disporre su
una scacchiera 3 torri, in modo che nessuna possa
"mangiare" le altre. In quanti modi si può
fare?
La prima torre può essere piazzata in ognuna delle 64
caselle (82 possibilità). Questa torre
minaccia 7 caselle in orizzontale e 7 in verticale, per un
totale di 14 caselle. La seconda torre allora non potrà
essere piazzata né in queste 14 caselle, né
naturalmente nella casella occupata dalla prima torre: le
restano 64-14-1 = 49 = 72 possibilità. Questa
seconda torre minaccia ancora 14 caselle, ma due le ho
già contate con la prima torre. Per la terza torre devo
quindi escludere 14 +12 caselle minacciate, più 2
occupate. Ne restano 36 = 62. In totale avrei
82·72·62
possibilità, ma devo tenere conto che le tre torri sono
indistinguibili, per cui una loro permutazione non modifica
nulla. In totale si ha allora
82·72·62/3! =
(8·7·6)2/3! = 18816. La formula trovata
si presta ad una facile generalizzazione. Con cinque torri avrei
(8·7·6·5·4)2/5! = 376320
possibilità.
Esercizio 5. Si devono disporre su una
fila di 10 sedie cinque coppie uomo-donna. In quanti modi la
cosa si può fare se la disposizione può essere
fatta alla rinfusa? E se le donne e gli uomini devono rimanere
vicini tra di loro? E se le coppie devono rimanere unite?
Nel primo caso ci sono 10! (3628800) possibilità. Nel
secondo si tratta di calcolare le possibili permutazioni dei
maschi (5!), delle femmine (ancora 5!) e dei due gruppi (2!):
28800 possibilità. Nell'ultimo caso di tratta di
permutare ciascuna coppia nei 2! modi possibili e poi le 5
coppie nei 5! modi possibili: 480 possibilità.
Esercizio 6. In una classe di 22
studenti, di cui 12 femmine e 10 maschi, si deve formare un
gruppo per una ricerca costituito da 3 maschi e 3 femmine. In
quanti modi la cosa si può fare se nei dieci maschi ci
sono due gemelli e si decide che non possano stare insieme?
Se non ci fosse alcuna restrizione il numero delle scelte
possibili sarebbe
C12,3·C10,3 =
26400. Il numero delle possibilità tra le femmine non
è alterato dalla restrizione. Tra i maschi basterà
che contiamo in quanti modi si può operare una scelta che
contenga i due gemelli: questo numero andrà sottratto dal
totale delle possibili scelte tra i maschi. E' immediato che
se un gruppo di 3 maschi deve averne due predefiniti (i
gemelli), restano 10-2 possibilità di scelta. Il numero
cercato è allora
C12,3·(C10,3 - 8)
= 24640.
Esercizio 7. In quanti modi n
palline indistinguibili possono venire collocate in n
celle numerate, in modo che esattamente una cella rimanga vuota?
Che cosa cambia se le palline sono distinguibili?
Bisogna innanzitutto scegliere la cella vuota (si può
fare in
n modi). Successivamente si deve collocare
almeno una pallina nelle restanti
n-1 celle e poi
scegliere una cella dove collocare due palline (si può
fare in
n-1 modi). In totale la collocazione si
può fare in
n(n-1) modi. Se invece le palline
sono distinguibili, dopo aver scelto la cella vuota e quella che
deve contenere due palline, cosa che si può fare in
n(n-1) modi come prima, occorre ancora scegliere quali
palline mettere nelle varie celle. Ci sono
Cn,2 modi di scegliere le due
palline da mettere nella cella che le conterrà, e poi
(
n-2)! modi di distribuire le restanti palline nelle
restanti celle. In totale ci sono
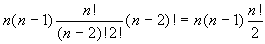
modi per collocare le palline come richiesto.
Esercizio 8. Se da un campione di
n oggetti in cui ve ne sono k di difettosi se
ne prendono a caso m, quante sono le possibilità
che ci siano i pezzi difettosi (≤k e
≤m)?
E' un problema classico di controllo di qualità a
campione. Intanto si possono scegliere
i oggetti
difettosi tra i
k in
Ck,i modi. In
un'estrazione di
m pezzi, ciascuno di questi
campioni difettosi si potrà combinare con uno costituito
da oggetti tutti non difettosi: la scelta si può fare in
C(n-k),(m-i) modi. Basterà fare il
prodotto di questi due numeri per avere il numero richiesto:
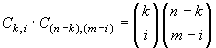
.
Esercizio 9. Se si lancia 8 volte un
dado, in quanti modi si possono ottenere 4 coppie diverse di
numeri uguali?
Intanto bisognerà scegliere 4 tra i sei numeri che
compaiono nelle facce di un dado: ciò si può fare
in C6,4 modi diversi, ovvero in 15 modi.
Fissata ora la scelta delle coppie, per esempio quelle formate
dai numeri 1,2,3,4, dobbiamo contare in quanti modi compaiono,
in qualunque ordine, due "1", due "2", due
"3", due "4" su otto caselle: si tratta
delle permutazioni di otto oggetti divisi in quattro gruppi da
2, P2,2,2,28 = 2520. In totale
37800 modi.
Esercizio 10. 3 ragazze e 2 ragazzi si
siedono a tavola in cinque posti consecutivi. In quanti modi
possono sedersi se ogni femmina vuole avere a fianco almeno un
maschio e viceversa?.
La cosa più semplice da fare è tracciare uno
schema ad albero ("grafo") esaminando le varie
possibilità. Si può partire da un maschio o da una
femmina e si ottiene:
|
M
|
M
|
|
|
|
no
|
|
|
F
|
M
|
F
|
F
|
no
|
|
|
F
|
F
|
M
|
F
|
|
|
|
F
|
F
|
F
|
|
no
|
|
F
|
M
|
M
|
F
|
F
|
no
|
|
|
M
|
F
|
M
|
F
|
|
|
|
M
|
F
|
F
|
M
|
|
|
|
F
|
|
|
|
no
|
Dunque le uniche possibilità sono MFFMF (e qui ho 2
possibilità di scelta al primo posto, 3 al secondo, 2
al terzo e 1 per i due rimanenti, in totale 12), FMFMF (e qui
ho 3 possibilità di scelta al primo posto, 2 al
secondo, 2 al terzo e 1 per i due rimanenti, in totale 12),
FMFFM (e qui ho 3 possibilità di scelta al primo
posto, 2 al secondo, 2 al terzo e 1 per i due rimanenti, in
totale 12). In totale 36 possibili disposizioni.
copyright 2000 et seq. maddalena falanga & luciano battaia
pagina pubblicata il 07/05/2004 - ultimo aggiornamento il
30/08/2004