Box counting

Riprendiamo in esame il quadrato di lato 1 che abbiamo già considerato nella introduzione della autosimilarità. Poiché il quadrato è un sottoinsieme del piano, lo rappresentiamo in un piano, che supponiamo di avere quadrettato con quadrati di lato s. Ci proponiamo di contare, al variare di s, il numero N(s) di quadretti occupati, magari parzialmente, dal nostro quadrato. Per rendere più semplice il calcolo consideriamo quadrettature di dimensione 1/2, 1/4, 1/8, ecc.; piazziamo inoltre il nostro quadrato in modo che non ci siano quadretti parzialmente occupati. E' chiaro che, in perfetta analogia con quello che abbiamo ottenuto nel caso dell'autosimilarità , potremo costruire la seguente tabella:

s	N(s)	In sostanza N(s)=s-2. Da qui possiamo concludere che la dimensione topologica del quadrato (cioè 2), si può ottenere con la stessa formula trovata nel caso dell'autosimilarità: .
1/2	4
1/4	16
1/8	64
s	s-2

Consideriamo ora un triangolo, isoscele e di lato 1 per semplicità, e applichiamo lo stesso procedimento.

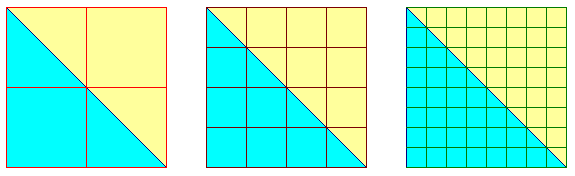
La tabella che che si costruisce ora è la seguente:

s	N(s)	Se calcoliamo il rapporto di prima, , otteniamo: , un risultato decisamente orribile e che sembra avere poco a che fare con la dimensione 2 che vorremmo attribuire anche a questo triangolo. E' evidente che ci aspettavamo qualche problema, per il fatto che il triangolo non si lascia quadrettare esattamente come il quadrato, ma capiamo facilmente che i problemi dovrebbero calare al diminuire delle dimensioni dei quadretti. Se infatti proviamo a calcolare il limite, quando s tende a 0, otteniamo esattamente 2.
1/2	3
1/4	10
1/8	36
s	(s+1)/(2s2)

Chi ha problemi con il calcolo dei limiti può trovare un calcolo approssimato, con il foglio elettronico.

La cosa comincia a piacerci: forse questo è un modo alternativo per definire la dimensione di un oggetto. Proviamo ad applicarla al nostro, ormai famoso, insieme di Cantor C. In questo caso, invece di quadratini potremo usare segmenti, in quanto il nostro insieme sta sulla retta. La stessa costruzione dell'insieme di Cantor rende immediato il calcolo. Possiamo partire con un fattore di scala 1/3 e l'insieme sarà contenuto in 2 segmenti; se passiamo ad un fattore 1/9, l'insieme sarà contenuto in 4 segmenti. In generale, con un fattore di scala di 1/3ⁿ, l'insieme sarà contenuto in 2ⁿ segmenti. Si trova immediatamente che è costante, come nel caso del quadrato, per cui non c'è nemmeno bisogno di fare un limite: , esattamente come con l'autosimilarità. 

Osserviamo che la tecnica descritta negli esempi di sopra non richiede che la figura considerata sia autosimile, e può venire facilmente applicata a figure anche molto complesse, in particolare con l'uso di strumenti automatici di calcolo.

Nella figura qui sotto sono rappresentati il grafico in questione per il caso del triangolo e, per confronto, il grafico della retta y=-2x. Si può vedere che, a parte il tratto iniziale, all'infinito i due grafici sono praticamente identici e la pendenza tende a -2, come calcolato sopra.

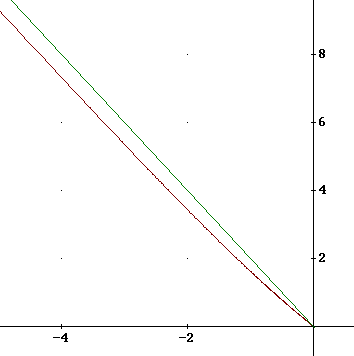
Si può ora dare la seguente definizione:

Data una figura nello spazio si considera una suddivisione dello spazio ambiente in cubi (eventualmente quadrati o segmenti se la figura appartiene ad un piano o ad una retta) di lato s e si calcola il numero N(s) di cubi anche parzialmente occupati dalla figura. Si chiama dimensione, basata sul box counting, (box counting dimension) la pendenza limite del grafico di logN rispetto a logs, quando s tende a zero e quindi logs tende a meno infinito. (Naturalmente nel caso che una tal pendenza limite esista!). 

Si tratta di un metodo alternativo per introdurre un concetto di dimensione per gli oggetti, metodo che si può applicare a qualsiasi oggetto. Per gli oggetti autosimili fornisce lo stesso valore della dimensione basata sull'autosimilarità. Anche a questa dimensione si dà il nome di dimensione frattale, e per essa si possono ripetere le considerazioni già fatta nel caso dell'autosimilarità .

C'è però un problema. Consideriamo per esempio l'insieme dei razionali contenuti tra zero ed 1 e proviamo ad applicare questo metodo. Se consideriamo suddivisioni del segmento [0,1] in segmenti di ampiezza s, l'insieme in questione si troverà sparso in tutti gli 1/s segmenti ottenuti, in quanto i razionali sono densi nei reali. Allora N=1/s. Ma da questo segue che =1: decisamente troppo, per quello che cerchiamo, per un insieme così povero di punti come l'insieme dei razionali compresi tra zero ed uno. In termini più tecnici, seppure ancora abbastanza intuitivi, si può dire che questo sistema per calcolare la dimensione frattale di un oggetto è troppo sensibile alla presenza di punti di accumulazione e quindi fornisce spesso dimensioni troppo grandi.

Nonostante questa, e altre, difficoltà questo concetto di dimensione è molto utilizzato, in quanto consente facili calcoli rigorosi in molte situazioni e accurate stime numeriche in altre, principalmente utilizzando la rappresentazione cartesiana che consente di estrapolare il valore della pendenza richiesta anche con un numero non grande di misure. La sua introduzione risale agli anni intorno al 1920.