Autosimilarità e dimensione
Cominciamo ora ad affrontare il problema della cosiddetta dimensione frattale. Una comprensione precisa di questo concetto non è semplice e richiede la conoscenza di tecniche matematiche abbastanza sofisticate. Ci proponiamo di avvicinarci il più possibile, e per gradi successivi, almeno limitatamente ad alcune situazioni semplici.
Consideriamo un segmento AB e sezioniamolo in parti con un fattore di scala s=1/2: otterremo N=2 segmenti identici e simili all'originale. Se utilizziamo invece un fattore di scala s=1/3, otterremo N=3 segmenti identici e simili all'originale, e così via.
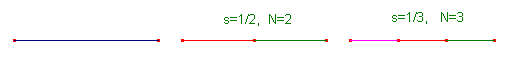
Se facciamo lo stesso procedimento su un quadrato, con s=1/2 otteniamo N=4 pezzi, con S=1/3 otteniamo N=9 pezzi.
.
Se infine ripetiamo lo stesso procedimento su un cubo otteniamo N=8 con s=1/2, N=27 con s=1/3, e così via.
Si constata immediatamente che, se indichiamo con d la
usuale dimensione topologica di questi oggetti, vale la seguente
formula: N=s-d, ovvero 
, con il logaritmo preso in una base qualunque.
Tentiamo ora di applicare la stessa tecnica all'insieme di
Cantor. Se sezioniamo l'insieme in parti con un fattore di
scala 1/3, otteniamo 2 parti identiche e simili
all'originale, se sezioniamo con un fattore di scala 1/9
otteniamo 4 parti identiche e simili all'originale, e
così via. Osserviamo che anche ora, come prima, il
rapporto 
è costante (vale
precisamente log2/log3
0.6309),
solo che questo rapporto non è più intero ed
è strettamente più grande della dimensione
topologica dell'insieme di Cantor che è zero.
Proviamo a ripetere il calcolo con il merletto di Koch: se
sezioniamo con un fattore 1/3 otteniamo 4 parti identiche e
simili all'originale, se usiamo un fattore 1/9 otteniamo 16
parti identiche e simili all'originale, e così via.
Questa volta il rapporto , ancora costante, vale log4/log31.2619. Anche ora il rapporto è non intero e
strettamente maggiore della dimensione topologica della curva
che è uno.
Comincia a venirci il sospetto che questi rapporti abbiano un ben preciso significato e che sia giustificato attribuire loro un nome specifico che ricordi la somiglianza con la formula della dimensione valida per segmento, quadrato e cubo. In realtà il fatto che per l'insieme di Cantor questo numero sia maggiore di zero soddisfa una certa idea intuitiva che ci fa pensare che la dimensione zero, attribuita con il metodo tradizionale, sia un po' troppo poco per un insieme che ha così tanti punti. Analogo discorso per il merletto di Koch, dove il fatto che questo rapporto sia maggiore di uno è in accordo con l'idea intuitiva che l'oggetto sia un po' più di una curva, anche se non è chiaramente una superficie, che avrebbe dimensione due.
Si dà la seguente definizione, valida per tutte le figure totalmente autosimili:
Si
chiama dimensione di un
oggetto, basata
sull'autosimilarità , il rapporto , dove N è il numero di copie che si
ottengono sezionando l'oggetto con un fattore di scala s.
La precisazione basata sull'autosimilarità è importante perché, come già vista, questo numero può essere diverso dalla dimensione topologica e perché, come vedremo, esistono altri metodi per introdurre un concetto di dimensione per questi oggetti. La definizione appena data è uno dei metodi, ma non l'unico, per introdurre la cosiddetta dimensione frattale. L'aggettivo frattale è dovuto al fatto che essa può essere espressa da un numero non intero.
E' opportuno, per sgomberare il campo da equivoci, segnalare che il concetto di dimensione frattale appena introdotto è completamente diverso da quello usuale di dimensione topologica e il fatto che si usi lo stesso nome non deve trarre in inganno. La dimensione topologica continua ad avere un chiaro e preciso significato, solo che oltre a questo numero che caratterizza una determinata proprietà degli oggetti, ora ne abbiamo considerato un altro, che caratterizza un'altra proprietà degli stessi oggetti. Rispetto a questa nuova proprietà che abbiamo ora preso in esame succede che per alcuni oggetti il numero che la rappresenta è lo stesso della dimensione topologica, per altri no: nel primo gruppo rientrano il segmento, il quadrato, il cubo, nel secondo la Polvere di Cantor, il merletto di Koch, e altri che considereremo più avanti.
Si può dare ora la seguente definizione:
Si chiama
frattale un
oggetto autosimile per cui la dimensione frattale è
strettamente maggiore di quella topologica.
Nessuna "meraviglia" se esistono oggetti che hanno una dimensione non intera: fin quando li si esamina da un certo punto di vista essi possono avere al massimo dimensione tre, e la dimensione deve essere intera; quando invece si esaminano altre caratteristiche degli stessi oggetti, possiamo loro attribuire, oltre al numero che qualifica se sono solo lunghi, o anche larghi o anche alti, anche un altro numero, che può essere non intero, e che misura, se così possiamo dire, il loro livello di autosimilarità . Non vale dunque la pena di usare punti esclamativi quando ci si accorge che, per certi oggetti, la dimensione frattale è, appunto, non intera.
Osserviamo che la definizione di dimensione frattale aggiunge, per ora solo per gli insiemi autosimili, un nuovo numero tra quelli che possiamo collegare agli insiemi di punti dello spazio, numero che va ad aggiungersi alla cardinalità e alla dimensione. Per fare un esempio possiamo raggruppare quanto finora detto nella seguente tabella:
| Segmento | Quadrato | Cubo | Insieme di Cantor | Merletto di Koch | |
| Cardinalità |
 1
|
1
|
1
|
1
|
1
|
| Dimensione | 1 | 2 | 3 | 0 | 1 |
| Dimensione frattale | 1 | 2 | 3 | 0.63 | 1.26 |
Si noti come a numeri uguali su una certa riga possano corrispondere numeri diversi su un'altra riga, in relazione alla diversa proprietà esaminata.
Il vero problema di questa definizione di dimensione è però che si applica solo a figure autosimili; per questo cerchiamo di affrontare il problema con un'altra prospettiva.