Lunghezza di un arco di curva piana
Senza entrare nei dettagli e limitandoci a considerazioni intuitive e manifestamente non rigorose vogliamo "dimostrare" la formula per calcolare la lunghezza di un arco di curva piana che sia grafico di un funzione reale di variabile reale. Supporremo che la funzione, f(x), sia derivabile con derivata continua in un intervallo [a,b].
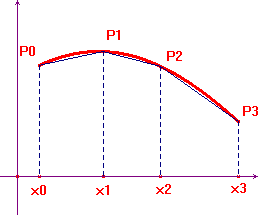
Considerando una suddivisione di [a.b] in intervalli
"infinitamente piccoli" dx, potremo ritenere
che la lunghezza della curva coincida con quella della spezzata
di lati individuati dagli estremi 
e
, con i = 0,1, 2, ... , n.
La lunghezza di questa spezzata è: 
.
La supposta derivabilità della funzione ci consente di
applicare il teorema di Lagrange, da cui otteniamo 
, ovvero, se l'ampiezza degli intervalli tende
a zero, 
.
Questa formula richiede il calcolo di un integrale solitamente non facile, nondimeno è importante perché mostra come la teoria dell'integrale di Riemann possa risolvere numerosi problemi di misura, e non solo quello della misura dei domini piani.
Forniamo, senza alcuna giustificazione, anche le due formule seguenti.
Se la curva è data in forma parametrica 
, con f e g funzioni derivabili di
t, la lunghezza dell'arco di curva compreso tra i
valori a e b del parametro è data da
.
Se infine la curva è data mediante la sua equazione
polare ρ=ρ(θ), con variabile tra a
e b, la lunghezza è data da 
.
Esempio
Calcolare la lunghezza del grafico della funzione 
nell'intervallo [0,5].
Poiché 
, applicando la formula
precedente si ha: 
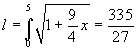. Per il calcolo
della primitiva si procede nel seguente modo: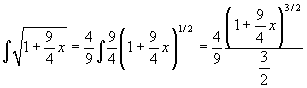 
.