I teoremi di Guldino
I due teoremi di questa pagina portano il nome di Paul Guldin, matematico svizzero (1577-1643), ma in realtà sono già riportati nel libro VII della Collezione di Pappo di Alessandria e costituiscono il più generale risultato di Analisi infinitesimale dell'antichità che si conosca.
Essi contengono due interessanti formule atte a calcolare il baricentro di linee e di superfici.
Baricentro di un arco di curva omogeneo
Riscriviamo le formule che ci hanno condotto ad ottenere
l'area della superficie laterale
di un solido di rotazione, indicando con li
la lunghezza di un lato della spezzata, con
yi l'ordinata del punto medio del lato
della spezzata, con Si l'area della
superficie laterale del tronco di cono, con L la
lunghezza dell'arco di curva. Indichiamo poi con G
il baricentro dell'arco di curva, pensato omogeneo.
L'ordinata y del baricentro può essere
approssimata con 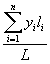 .
L'area della superficie laterale del solido di rivoluzione
si può approssimare allora con
.
L'area della superficie laterale del solido di rivoluzione
si può approssimare allora con 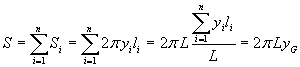 .
La formula varrà senza approssimazione se la lunghezza
dei lati della spezzata tende a zero; essa esprime il
primo teorema di Guldino:
.
La formula varrà senza approssimazione se la lunghezza
dei lati della spezzata tende a zero; essa esprime il
primo teorema di Guldino: ![]() .
.
La formula permette di ricavare l'ordinata del baricentro della linea, se si riesce a calcolare S ed L. Per calcolare l'ascissa basterà eseguire una rotazione attorno all'asse y.
Baricentro di un dominio piano
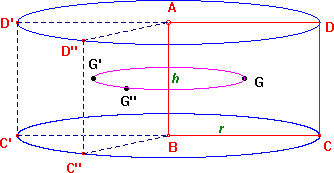
Consideriamo ora un cilindro circolare retto, ottenuto per
rotazione di un rettangolo ABCD attorno al lato AB. Indichiamo
con h l'altezza del cilindro (=AB) e con r
il raggio di base (=BC). Indichiamo poi con G il baricentro del
rettangolo, supposto omogeneo; G dista r/2 da AB.. Per
il volume del cilindro si ha allora: ![]() ,
ove A è l'area del rettangolo.
,
ove A è l'area del rettangolo.
Si può cioè concludere che il volume è dato dall'area del rettangolo per la lunghezza della circonferenza descritta dal baricentro del rettangolo stesso.
Riprendiamo ora in esame il procedimento utilizzato per
calcolare il volume di un solido di rotazione, che si ottiene
facendo la somma dei volumi di tanti cilindri (infinitamente
sottili). Detta yGi l'ordinata del
baricentro del generico rettangolo (che si trova a metà
dell'altezza del rettangolo), possiamo scrivere la seguente
formula approssimata per il volume del solido di rotazione: 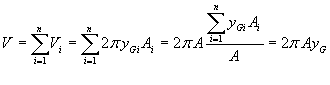 , dove A è l'area totale del
trapezoide e
, dove A è l'area totale del
trapezoide e ![]() è l'ordinata
del baricentro del trapezoide stesso. Dunque
è l'ordinata
del baricentro del trapezoide stesso. Dunque ![]() ,
in perfetta analogia con la formula relativa al baricentro di
una linea piana: questa formula esprime il secondo
teorema di Guldino.
,
in perfetta analogia con la formula relativa al baricentro di
una linea piana: questa formula esprime il secondo
teorema di Guldino.
La formula permette di ricavare l'ordinata del baricentro del dominio piano, se si riesce a calcolare V ed A. Per calcolare l'ascissa basterà eseguire una rotazione attorno all'asse y.
Esempi
-
Calcolare il baricentro di un semicerchio. Se consideriamo un
sistema cartesiano con origine nel centro del semicerchio e
asse x coincidente con il suo diametro, per ragioni
di simmetria concludiamo che l'ascissa del baricentro
è zero. Per l'ordinata possiamo applicare il
secondo teorema di Guldino, tenendo conto che la rotazione
del semicerchio dà luogo ad una sfera. Si ottiene:
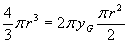 , da cui
, da cui 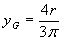 .
.
-
Calcolare il baricentro di una semicirconferenza. Con le
stesse notazioni dell'esempio precedente, l'ascissa
del baricentro è sempre zero, mentre per
l'ordinata usiamo il primo teorema di Guldino, tenendo
conto che la rotazione della semicirconferenza dà
luogo ad una superficie sferica. Si ottiene:
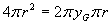 , da cui
, da cui 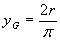 .
.