Area di un dominio piano
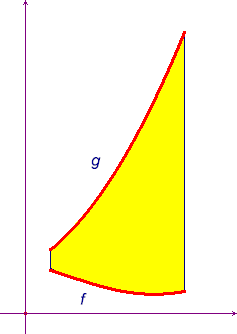
Date due funzioni f e g integrabili in un intervallo [a,b], con f<g, consideriamo la regione del piano cartesiano xOy compresa tra i grafici delle due funzioni e le rette x=a, x=b. La chiameremo un dominio piano normale rispetto all'asse x.
E' immediato (tenendo conto di come abbiamo definito l'area di un trapezoide) che la sua area è data dal seguente integrale di Riemann:
,
cioè dall'integrale della funzione superiore meno quello della funzione inferiore. La formula vale anche se le funzioni non sono strettamente positive.
Esempi
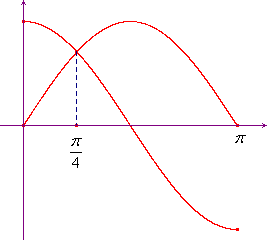
1 - Calcolare l'area del dominio piano delimitato dalle funzioni sinx e cosx nell'intervallo [0,π].
Se si tiene conto che le due funzioni si intersecano per 
, si trova subito che l'area richiesta è:
.Il calcolo
è immediato e si ottiene: 
.
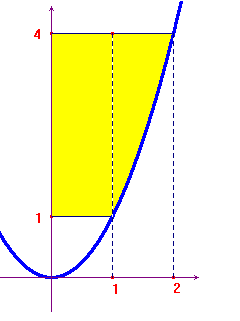
2 - Data la parabola y=x2 calcolare l'area della regione piana finita delimitata dalla curva, dall'asse delle y e dalle rett y=1, y=4.
Occorre dividere la regione in un rettangolo (di area 3) e in un dominio limitato dalla retta
y=4 e dalla parabola, nel tratto [1,2], la cui area è: 
. In totale l'area vale
.
Per evitare di dividere la regione in due parti si poteva osservare che essa poteva essere vista
come dominio normale rispetto all'asse y (addirittura come
un trapezoide rispetto a questo asse), delimitato dall'asse y e dalla funzione 
. Si sarebbe ottenuto:
, cioè
esattamente lo stesso valore.