Che cosa significa dimostrare?
Secondo la definizione che abbiamo dato, dimostrare significa dedurre, mediante ragionamento logico basato su assiomi o teoremi precedenti, la tesi dall'ipotesi. L'idea che sta alla base di questo concetto è che un qualsiasi studioso deve poter essere in grado di seguire e rifare tutti i ragionamenti utilizzati, se conosce i "precedenti" (cioè quello che è già stato assunto o dimostrato). Ovvero: la dimostrazione è un ragionamento mediante il quale un matematico può convincere un altro matematico, che la legga, della verità di una affermazione.
Questa idea di dimostrazione è essenzialmente contenuta negli Elementi di Euclide, anzi quest'opera è (seppure con qualche sbavatura) il primo e più famoso esempio di costruzione di una teoria basata unicamente su alcune assunzioni e su ragionamento: introdotti gli enti primitivi e i postulati, lo studioso potrebbe chiudersi in una stanza e riscrivere l'intero testo, senza mai fare ricorso a idee o concetti del mondo reale.
Dimostrare nella matematica pre-classica
All'inizio della storia della matematica è
chiaro che dimostrare aveva un significato completamente
diverso. Consideriamo per esempio il problema della somma degli
angoli interni di un triangolo. E' abbastanza facile provare
sperimentalmente che detta somma, in un triangolo equilatero,
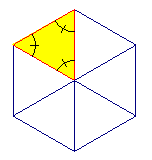
è un angolo piatto. Infatti utilizzando mattonelle con
questa forma (e forse è proprio così che la
"dimostrazione" fu fatta) è facile ricoprire un
pavimento e in particolare si possono costruire figure come
quella qui a lato. Siccome occorrono sei mattonelle triangolari
per coprire tutto l'angolo giro, ciascuno degli angoli al
centro deve essere un sesto dell'angolo giro: se ne deduce
che la somma dei tre angoli del triangolo deve essere tre sesti
di angolo giro, cioè un angolo piatto.
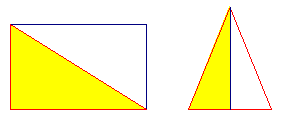In modo analogo si può ragionare su un triangolo
rettangolo (che è la metà di un rettangolo, in cui
la somma degli angoli è banalmente quattro retti) o in un
triangolo isoscele (basta dividerlo a metà in due
triangoli rettangoli mediante l'altezza). Procedendo su
questa strada si può anche considerare un triangolo
qualunque, dividendolo in due triangoli rettangoli mediante una
delle altezze che è sicuramente interna al triangolo
stesso, ma è chiaro che si tratta di un procedimento
basato su considerazioni visive di triangoli che possono cadere
sotto la nostra esperienza sensibile: che ne sarebbe di un
triangolo enorme i cui vertici siano tre stelle fisse, figura
che non può essere chiaramente disegnata su carta? Molto
diverso è il modo, che chiamiamo razionale, in
cui Euclide (o i suoi predecessori, visto che Euclide raccoglie
nella sua opera tutti i risultati già noti e dimostrati)
affronta il problema: se tra i punti, le rette, ecc. valgono
certe relazioni, allora posso definire un triangolo e,
solo sulla base di quelle relazioni e senza riferimento ad
alcuna situazione concreta, posso concludere che la somma degli
angoli interni deve essere un angolo piatto.
E' interessante osservare che nel metodo razionale il problema del triangolo equilatero di cui abbiamo parlato sopra non si pone nemmeno: se l'oggetto costruito nel modo detto è un triangolo, e se gli assiomi che io ho scelto sono validi, la somma degli angoli interni deve essere un angolo piatto. Si noti che oggi noi sappiamo che ad oggetti di questo tipo non si può applicare la geometria classica (per cui non è detto che il risultato sulla somma degli angoli interni si possa applicare), ma questo è un altro problema: nella teoria euclidea è corretto dedurre che la somma degli angoli interni di un triangolo è un angolo piatto, mentre il fatto che poi questo risultato possa essere applicato a oggetti del mondo reale è un problema di cui il geometra non si interessa affatto.
Come accennato, il concetto di dimostrazione quale risulta dal lavoro di Euclide, con le precisazioni scaturite dagli studi posteriori, è ancora quello che noi oggi riteniamo valido, ma ci sono alcune importanti osservazioni da fare: ne sceglieremo due, una che prende spunto da un teorema sui gruppi e una che prende spunto dal cosiddetto teorema dei quattro colori.
Il caso del "teorema enorme"
Si tratta del famoso teorema di classificazione dei gruppi semplici. Non vogliamo entrare nei dettagli del suo contenuto, cosa che del resto sarebbe impossibile in questo contesto; quello che qui ci interessa segnalare è legato al nome con cui è spesso citato: il "teorema enorme". Si tratta senza dubbio del più grande teorema che la matematica abbia mai conosciuto: la dimostrazione originale occupa circa 15000 (si, proprio quindicimila) pagine sparse in oltre cinquecento articoli di riviste di matematica, e ha richiesto il contributo di un centinaio di matematici e quarant'anni circa di lavoro. Un gruppo di ricercatori sta oggi lavorando per ridurre questa sterminata mole di materiali a dimensioni più ragionevoli, ma pare che non si potrà andare al di sotto delle cinquemila pagine. La dimostrazione di questo teorema soddisfa nella sostanza l'idea che noi abbiamo di dimostrazione, ma è altamente improbabile che possa essere rifatta da una sola persona, seguendo rigorosamente il metodo del ragionamento ipotetico-deduttivo (a meno che uno non voglia fare solo questo nella sua vita!).
E' interessante, a questo proposito, quanto scrive Michael Aschbacher, l'uomo che contribuì in maniera decisiva alla dimostrazione (citazione presa dal testo di Keith Devlin riportato in bibliografia):
Io sono scettico sulla possibilità che possa mai apparire in futuro una dimostrazione breve (di questo teorema) di qualsiasi tipo. Le dimostrazioni lunghe infastidiscono i matematici. Da un lato più la dimostrazione è lunga, maggiore è la probabilità di errore. La probabilità di errore nella dimostrazione del teorema della classificazione è praticamente uguale ad 1. D'altro canto la probabilità che non si riesca a correggere ogni singolo eventuale errore è praticamente zero, e poiché la dimostrazione è finita, la probabilità che il teorema sia sbagliato è prossima a zero. Con il passar del tempo e con la possibilità di assimilare la dimostrazione, il grado di affidabilità può solo aumentare. Forse è anche il caso di considerare la possibilità che esistano teoremi naturali fondamentali che possono essere formulati in modo conciso, ma che non ammettono una dimostrazione breve e semplice. Ho la sensazione che il teorema di classificazione sia uno di questi. Man mano che la matematica diventa più sofisticata, sarà sempre più probabile imbattersi in teoremi del genere.
E' evidente, alla luce di queste parole, che la nostra idea di dimostrazione deve essere per lo meno "ricalibrata": sarebbe stato chiaramente inconcepibile, nel testo di Euclide, parlare di probabilità che un teorema possa essere sbagliato.
Segnaliamo esplicitamente che questo teorema, di enorme importanza teorica, ha applicazioni pratiche nei campi più disparati. Citiamo solo la progettazione di sistemi di codici autocorrettori, cioè metodi per codificare le informazioni in grado di compensare le distorsioni e le perdite occasionali.
Solo a titolo di curiosità, per chiarire almeno in parte una delle difficoltà della dimostrazione, ricordiamo che nel corso dei lavori ci si è trovati a trattare un gruppo con 808017424794512875886459905961710757005754368000000000 elementi (circa 8·1053!).
E' abbastanza significativo notare quanto questo teorema, per la sua complessità, sia diverso dal famoso teorema di Euclide sull'infinità dei numeri primi, un modello praticamente insuperato di concisione ed eleganza in matematica!
Il teorema dei "quattro colori"
Il problema del numero minimo di colori necessari per colorare una qualunque carta geografica nasce da un'osservazione quasi casuale di Francis Guthrie (il problema è, per questo, anche noto come problema di Guthrie) nel 1852 e diventa un problema "ufficiale" nel 1878, quando Arthur Cayley ne parla in una riunione della London Mathematical Society. La dimostrazione che quattro colori sono sempre sufficienti, dopo una lunga serie di insuccessi e di false dimostrazioni (una delle più famose è quella di Alfred Bray Kempe, pubblicata nel 1879 e demolita da Percy John Heawood una decina d'anni dopo), avviene ad opera di due matematici dell'Università dell'Illinois, Kenneth Appel e Wolfgang Haken, nel 1976.
La cosa interessante per noi non è la dimostrazione in sé, che non potremmo seguire, quanto il metodo utilizzato per arrivarci. Sorvolando sui dettagli e semplificando un po' (forse anche un po' troppo!), l'idea è questa: mediante una serie di ragionamenti e deduzioni logiche si riduce la prova ad un numero finito (purtroppo enorme) di casi e si fanno fare i conti su questi casi ad un calcolatore.
La cosa cruciale in questo modo di procedere è che il lavoro richiesto al calcolatore è tale che nessun essere umano potrà mai verificare a mano la correttezza del risultato: il concetto stesso di dimostrazione come noi lo abbiamo sempre pensato, viene a crollare. Come dice Keith Devlin, «La matematica, da quel momento, non è più la stessa. ... L'intero concetto di dimostrazione matematica è improvvisamente cambiato e un'eventualità profilatasi minacciosamente fin dall'epoca dei primi sviluppi degli elaboratori elettronici, all'inizio degli anni cinquanta (del 1900!), si è finalmente concretizzata: il calcolatore ha soppiantato il ricercatore nella costruzione di una parte di una dimostrazione matematica».
Anche qui riteniamo giusto segnalare che questo teorema, che ha impegnato i matematici per oltre centovent'anni, è importante non solo per motivi teorici, ma anche per le sue numerose applicazioni, in particolare nella teoria dei grafi e in tutto quello che ne consegue nell'informatica.
Il pesce d'aprile di Martin Gardner
Il primo aprile 1975 Martin Gardner pubblicò su Scientific American una mappa, affermando che non era possibile colorarla con soli quattro colori. La mappa è riportata qui sotto.
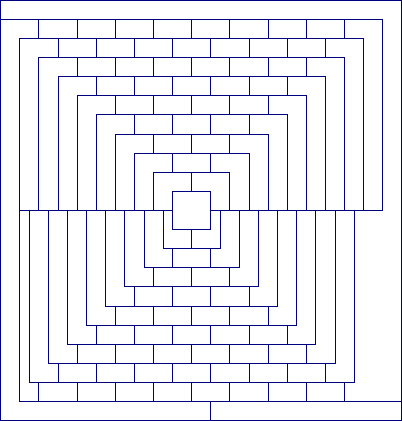
Considerata la data della pubblicazione i lettori si resero subito conto dell'inganno, e difatti la mappa si può colorare, seppure con qualche difficoltà. Puoi tentare di riuscirci, ma se proprio non ce la fai ti mostriamo la soluzione.
Bibliografia per questa pagina
- Keith Devlin, Dove va la matematica, Bollati Boringhieri, Torino 1994 (Uno splendido libro, di cui consigliamo vivamente la lettura, anche se alcuni argomenti sono decisamente un po' difficili).
- Paolo Musso, La Scienza e i miti, in http://digilander.libero.it/filosofiascienza/scimit2.htm