Problema 6 - Soluzione
Individuare i naturali x che godono della seguente proprietà: se si sopprime l'ultima cifra della loro scrittura decimale si ottiene un numero y che è un divisore di x.
(da Shklarsky D.O., Chentzov N.N., Yaglom I.M., The Ussr Olympiad Problem Book, Freeman and Company, San Francisco, 1962)
Primo schema di soluzione
Essendo y ottenuto dall'eliminazione dell'ultima cifra di x, esso apparterrà all'ordine di grandezza immediatamente più piccolo; per cui x=10y+u (dove u è l'ultima cifra di x: 0≤u<10).
Affinché y sia divisore di x, u dovrà essere un multiplo di y: u=ny e dunque x=10y+ny=(10+n)y
*) per n=0 si ha che u=0, y=0,
x=10y ( e cioè qualunque x terminante
per zero soddisfa le condizioni del problema)
**) per n≥1 u≥y;
essendo u di una sola cifra, allora y<10, e
quindi x<100; per cui in questo caso rientrano solo
numeri di due cifre.
Possiamo dunque affermare che l'insieme dei numeri che godono della proprietà richiesta è costituito da tutti i multipli di 10 e da tutti i numeri compresi tra 11 e 99 tali che l'ultima cifra, u, sia multipla della penultima, y. Questi ultimi numeri sono precisamente: 11, 12, 13,14, 15, 16, 17, 18, 19, 22, 24, 26, 28, 33, 36, 39, 44, 48, 55, 66, 77, 88, 99.
Soluzione di Marco Facchini, classe IIIB, Liceo Scientifico Grigoletti, A.S. 2000-2001
Secondo schema di soluzione
Possiamo scrivere i due numeri come: 
e
, con le note limitazioni per i numeri
a, b, ..., w, z. Se y è un divisore di
x, allora x=ky, con k>0 opportuno.
Utilizzando le scritture precedenti per i due numeri si
può allora ottenere:
(*)
Analizziamo ora i diversi possibili valori di k:
-
Se 0<k<10, allora nella formula (*) si ha una somma di numeri negativi che non può essere zero.
-
Se k=10, si ottiene subito da (*) che z=0: tutti i numeri che terminano per zero vanno bene.
-
Se k>10, poniamo k=10+m e otteniamo, per le espressioni tra parentesi in (*) ,
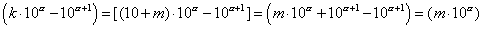. Ne segue che 
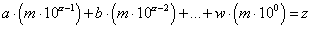; dato che deve essere z<10, si
conclude che 
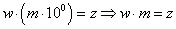. Dunque
l'ultima cifra del numero x deve essere multipla
della penultima.
Soluzione di Giovanni Pizzi, classe IIIB, Liceo Scientifico Grigoletti, A.S. 2000-2001