www.batmath.it
Saying maths 2 - Mainly numbers
Numbers: general remarks
- A point (.) is used for decimals, and not a comma (,); commas in figures are used only when writing thousands (example 10,000: ten thousand), but we prefer to avoid the use of commas in mathematical formulas.
-
Use of "and"
- to indicate the location of the decimal point: so 100.5 is one hundred and 5 tenths, but one hundred point five is by far more common; 239.36 is two hundred thirty-nine and thirty-six hundredths, but two hundred thirty-nine point three six is by far more common;
- in British English we use and when saying numbers in the hundreds: 105 is one hundred and five;
- in American English we do not use and when saying numbers in the hundreds: 105 is one hundred five;
- anyhow we have also found on the Internet something like this: 105 is hundred five;
- so, as what is "correct" changes with time, choose your standard and follow it!
-
The "0" (oh, nought, zero, love, nil)
-
oh
- after the decimal point: 27.05 is twenty-seven point oh five;
- in years: 1907 is nineteen oh seven;
- in telephone, bus, hotel room numbers (but this is not very important in maths!);
-
nought
- before the decimal point: 0.05 is nought point oh five (but see also the next heading);
- tip: noughts and crosses is a game like the Italian "filetto";
-
zero
- for the number 0 itself: "0" is zero;
- before a decimal point, mainly in American English, but also in British English: 0.05 is zero point oh five, instead of the more "traditional" form "nought point oh five";
- for the temperature: -7°C is seven degrees below zero, which you can also say minus seven;
-
nil
- in football scores: "Italy wins 3-0" is "Italy wins three nil" (also three to nil); sometimes nothing is used in the place of nil "3-0" can be three to nothing;
-
love
- in tennis games: "the score of the game is 15-0" is "the score of the game is fifteen love"; "0-0" is love all or love game.
-
oh
-
The decimal point
- the numbers after the decimal point are all read separately 0.0023 is nought point oh oh two three; use of "and" is also allowed (see the previous heading), but we prefer this way of saying numbers with a decimal point;
- you can also use shorter forms: 0.0005 can be read as nought point double oh oh five;
-
in periodic numbers we use "recurring":
5.376666... is five point three seven
-pause-six recurring, while 5.376376376... is five point three seven six-pause-all recurring; -
digits after the decimal point are (almost) always
grouped while reading currencies, lengths, and other
measures:
- £15.50 is fifteen pounds fifty / fifteen pounds fifty pence / fifteen fifty (if no misunderstanding can occur);
- €2.27 is two euro twenty-seven / two euro twenty-seven cents;
- 47.99s (seconds) is forty seven seconds ninety-nine hundredths;
- 3.87m (meters) is three meters eighty-seven centimetres.
-
Kinds of numbers
- natural, whole, integer, rational, irrational, real, complex (imaginary)
- odd, even
- fractional
- prime
- binary, octal, decimal, hexadecimal
- random
Numbers: elementary calculations
| = | The equals sign |
| x=3 ; x≠3 | x equals three / x is equal to three ; x (is) not equal to three |
| x≡y | x is equivalent to (or identical with) y |
| x>y ; x≥y | x is greater than y ; x is greater than or equal to y |
| x<y ; x≤y | x is less than y ; x is less than or equal to y |
| x<a<y | a is greater than x and less than y / a is between x and y / x is less than a and less than y |
| x≤a≤y |
a is greater than or equal to x and less than or
equal to y / a is between
x and y -pause- bounds
included / x is less than
or equal to a and less than or equal to y
|
| << ; >> ; <<< ; >>> | much less than ; much greater than ; very much less than ; very much greater than (The last two are not frequently used, but they are in the set of Unicode characters). |
| a+b=s (addition) | a and b are the addends, s is the sum, a and b are also the items of the addition. |
| a+b=s |
a plus b is (/ equals
/ is equal to)
s a and b is (/ equals / is equal to) s s is the sum of a and b |
|
a-b=d (subtraction or difference) |
a is the minuend, b is the subtrahend, d is the remainder or the difference |
| a-b=d |
a minus b is (/ equals
/ is equal to) d a take away b is (/ equals / is equal to) d d is the difference between a and b |
| a±b | a plus or minus b |
|
a×b=p, or a·b=p, or simply ab=p (multiplication) |
a and b are the factors or the multipliers, p is the product |
| a×b=p, or a·b=p, or simply ab=p |
a times b is (/ equals
/ is equal to) p a multiplied by b is (/ equals / is equal to) p a by b is (/ equals / is equal to) p a b is (/ equals / is equal to) p p is the product of a and b |
| a : b = q, or a / b = q (division) | a is the dividend, b is the divisor, q is the quotient or the ratio |
| a:b=q, or a/b=q |
a divided by b is (/
equals / is equal to)
q q is the quotient of the division of a by b |
| verbs concerning operations | to sum, to subtract / to deduct, to multiply, to divide |
 (fraction)
|
a is the numerator, b is the denominator (the outcome is always called the quotient, as in the division) |
|
|
a fraction can be said a divided by b (as a
normal division ), or a over b. Cardinal
numbers for the numerator and ordinal numbers for the
denominator are also used (as in Italian):  is a third,  is two thirds. Special cases
are  (a/one
half),  (a/one
quarter),  (three
halves),  (three
quarters), and similar. The special notation
sometimes used for improper fractions, as  , is said three and a
half.
|
Numbers: advanced calculations
| |x| or abs(x) | The absolute value of x |
| ab | a is the base, b is the index or the exponent |
| x2 | x squared / x (raised) to the power two |
| x3 | x cubed / x (raised) to the power three |
| x4 | x to the fourth / x (raised) to the power four |
| xn | x to the nth / x (raised) to the power n |
| x-n | x to the minus n / x (raised) to the power minus n |
|
root x / square root x / square root of x |
|
cube root x / cube root of x |
|
fourth root x / fourth root of x |
|
nth root x / nth root of x |
|
nth root -pause- x
cubed or nth root
-pause- of x cubed
|
|
x hat |
|
x bar |
|
x tilde |
|
x dot |
|
x dot dot / x double dot |
| n! | n factorial / factorial n |
|
n choose p |
| xi | x i / x subscript i / x suffix i / x sub i |
| xi (not a power!) | x index i / sometimes x i if no misunderstanding with xi can occur / x superscript i |
| (x+y)3 ; (x+y)n | x plus y all cubed ; x+y all to the nth |
| x3+y3 | x cubed plus y cubed |
| a1 + a2 + ... +an | a one plus a two and so on up to a (sub) n |
| a1 × a2 × ... ×an | a one times a two and so on up to a (sub) n |
|
the summation symbol |
|
the sum as i runs from zero to n of the x i / the sum from i equals zero to n of the x i |
|
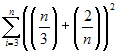
the sum -pause- as i
runs from three to n -pause-
of the quantity n over 3
-pause- plus the quantity 2 over
n -pause- all squared
(but probably nobody will understand what you mean if
he can't read the blackboard or the transparency!!)
|
|
parenthesis -pl. parentheses / round brackets |
|
brackets / square brackets |
|
braces / curly brackets |
| π | pi |
Useful expressions
- the noughts and ones of computer language: to refer to the digits used by computers ("0" and "1")
- the slashed zero: the zero of the computer
- to reset to zero
- to extract a root
- to cast out nines (the famous test for divisions)
- to move the decimal point back (or forward) two places
- readings accurate to two decimal places
- to round a number up or down to the nearest integer
- to calculate up to n decimal places
- to reduce to the lowest common denominator
copyright 2000 et seq. maddalena falanga & luciano battaia
first published on february 08 2003 - last updated on april 10 2020