www.batmath.it
Antiderivatives and Riemann integrals: some observations
The fundamental theorem of calculus sets a link between the concept of antiderivative and of Riemann integral:
- the Riemann integral
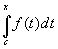is an antiderivative of the continuous function f; - given an antiderivative G(x) of a continuous function f we have:
.
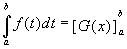Despite this important link, the two concepts remain quite different: the algorithm used to calculate antiderivatives produces a class of functions; the one used to calculate Riemann integrals produces a real number.
Besides this we want to point out the following facts.
- The set of all integral functions of a given continuous function f is, in general, a
subset of the set of all antiderivatives. An integral function is always zero at the starting
point:
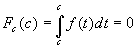, while an
antiderivative may be always strictly positive. For example the function
F(x)=x2+1 is an antiderivative of f(x)=2x, but it is nowhere zero:
this means that it can't be an integral function. - A function that has a jump discontinuity can't have antiderivatives, while it may be integrable. The simplest examples are step functions.
- The integral functions of a non continuous function usually are not antiderivatives. For
example
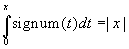, but the
function |x| is not an antiderivative, as it is not differentiable in zero. Observe that
this equality is an alternative definition of the absolute value function. - An unbounded function can't be Riemann integrable, while it may have antiderivatives. For
an example try to find the derivative, f(x), of
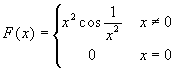. As f is unbounded it is certainly not Riemann
integrable, but obviously it has an antiderivative, the function F itself!
copyright 2000 et seq. maddalena falanga & luciano battaia
first published on january 07 2003 - last updated on september 01 2003