www.batmath.it
Final exercises
-
If t is a real number such that
0<t<2, calculate
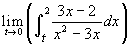 .
.
-
Given the function
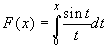 , find the points
where it gets a relative maximum. (The integral function is
supposed to be extended so that it is everywhere continuous).
, find the points
where it gets a relative maximum. (The integral function is
supposed to be extended so that it is everywhere continuous).
-
Solve the following inequality:
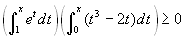 .
.
-
f is a function continuous together with its first
and second derivative; the tangents to the graph of
f in the numbers a and b create an
angle whose measure is, respectively, of π/3 and π/4
with he positive x-axis. Calculate the following two
integrals:
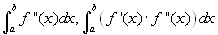 .
.
-
Given the function
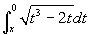 , find the
intervals where the function is increasing and those where
the function is convex.
, find the
intervals where the function is increasing and those where
the function is convex.
-
Given the function
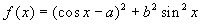 , find the values
of the numbers a and b such that
f(0)=0 and
, find the values
of the numbers a and b such that
f(0)=0 and 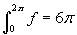 . Graph the
function.
. Graph the
function.
-
Calculate
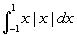 .
.
-
Given the function
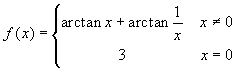 , calculate its
integral function with starting point -1. What can we say about
the derivative of this integral function?
, calculate its
integral function with starting point -1. What can we say about
the derivative of this integral function?
-
By direct calculation of the integral find the derivative of
the function
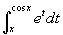 . Find again the same
derivative without calculating the integral.
. Find again the same
derivative without calculating the integral.
-
Find the domain of the following functions:
-
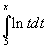 .
.
-
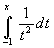 .
.
-
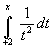 .
.
-
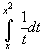 .
.
-
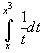 .
.
-
-
Prove that if f is an integrable function over
[-a,a] and f(-x)=-f(x) than
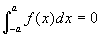 . Give a geometrical interpretation of this result.
. Give a geometrical interpretation of this result.
- The integral of a function is unchanged if we alter the values of a fucntion in a finite number of points. However this is no more true if we alter the function in a countably infinite number of points. Proof this with an example (sugg.: use Dirichlet's function).
copyright 2000 et seq. maddalena falanga & luciano battaia
first published on january 07 2003 - last updated on september 01
2003