The mean value theorem
Suppose that the function f(x) is non negative and
continuous in the closed interval [a,b]. Then the
Riemann integral 
exists and represents the
area bounded by the curve y=f(x) and the lines
y=0 (x-axis), x=a and x=b.
Consider a rectangle with bases on the x-axis between
a and b, and with the same area as the
integral. Then its height 
must represent the
mean value of the function. Of course, the restriction that the
function is non-negative (and also that of being continuous) is
not necessary and can be removed: they are only useful to
simplify geometrical interpretation.
Example The average value of the function f(x)=x2 on the interval [0,2] is 4/3 (remember we have proved that the integral is 8/3).
This property is generalized to integrable functions by the following
Mean value theorem
Suppose that f is integrable in the closed interval
[a,b]. Then there exists a number μ, with 
, such that 
. The number μ is
called the mean value of f in the
interval [a,b]. 
If the function f is continuous, there exists a number c in the interval [a,b] such that f(c)=μ. Unfortunately this theorem gives no hint in order to find the number μ, otherwise it would be conclusive as far Riemann integrals are concerned.
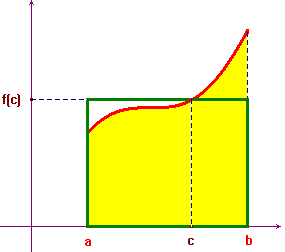
From a geometrical point of view this means that every trapezoid is equivalent to a rectangle: as any rectangle can be transformed in a square (by rule and compass), it's usual to say that every trapezoid can be squared.