The integral function
Consider an integrable function 
and two numbers c and x in [a,b].
Then the integral 
exists. If the number
c is fixed, the integral depends on x.
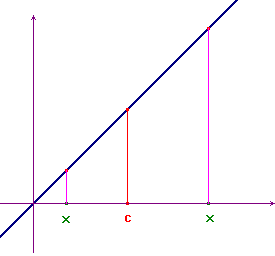
If, for example, f(x)=x the integral can be calculated by a simple geometrical method. You must only observe that the integral can be obtained by calculating areas of trapeziums or triangles, with the appropriate sign.
You always obtain: 
. The result is a new
function, that we call an integral function of
f, and represent by F(x): 
.
Observe, in the previous integral, that the
variable x is used in two different places:
- as the variable of the integrand function;
- as the upper bound of the integral.
In order to avoid confusion, usually one writes the same
integral using a different letter for the variable of the
integrand function: 
; in fact the variable of
the integrand function is not important, and any letter works.
This is a new way to construct functions. In some cases, as the previous example shows, the new function can be obtained by elementary methods, but we'll see that in many other cases the new function is not an elementary one, so this is a completely new technique to construct functions.
Obviously you could have considered the integral bounds in reverse order, but the function you obtain is simple the opposite one: -F(x).
You can also consider the composition technique to obtain more
functions; for example, slightly modifying the previous integral
you have: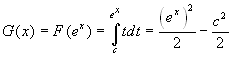 
. A still more complex
situation can be obtained, for example, as follows: 
.
The function f must be integrable between
c and x (or x and c,
if x is less than c). For example
the function 
, exists only for
x>0, while the function 
exists only for x<0.
Observe, in the example at the beginning of this page, that the
derivative of F(x) is f(x), and the lower
bound c of the integral is not important for this. We
may write: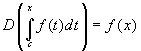 
, whatever is the point
c, provided the integral exists.
We give the following
Definition
Given an integrable function
and two numbers c and x in
[a,b], 
is the
integral function of f, with
starting point c. Sometimes it will be useful to
distinguish between integral functions with different starting
points: in these cases we'll use the notation
Fc(x), if c is the starting point.
This function plays a critical role in the theory of Riemann integrals.