Continuity
Roughly speaking: a function is continuous if we can draw its graph without lifting our pencil from the paper. This "definition" makes little sense from a mathematical point of view, so we investigate it with greater detail.
First of all the formal definition:
![]() Given a function
Given a function ![]() ,
and a point c in the domain
D, the function f is said to be
continuous at c if either c is not an
accumulation point for D, or, when c is an
accumulation point,
,
and a point c in the domain
D, the function f is said to be
continuous at c if either c is not an
accumulation point for D, or, when c is an
accumulation point, ![]() .
.
Important remarks
The point c must be in the domain of the function.
The value l that we used in the definition of limit
is now replaced by f(c).
Unlike the case of limits, here we do not want to investigate the behaviour of a function as x gets closer and closer to a given point c; on the contrary we want to check if the function approaches exactly the value f(c) as x approaches c.
Observe that, if c is a left (right) end point in the
domain, we need to check only ![]() (
(![]() ).
).
It's easy enough to prove that all elementary functions are continuous whatever point you take in the domain. So in order to find interesting examples we'll often use other kinds of functions, mainly functions defined in pieces.
-
Example 1: Consider the function
f(x)=sgn(x). As
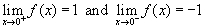 ,
the limit as x approaches zero does not exist, so
the function can't be continuous. If you examine the
graph, you can easily understand what we mean when saying
"the graph can't be drawn without lifting our
pencil from the paper".
,
the limit as x approaches zero does not exist, so
the function can't be continuous. If you examine the
graph, you can easily understand what we mean when saying
"the graph can't be drawn without lifting our
pencil from the paper".
-
Example 2: Consider the function
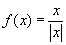 and the point c=0. Does it make sense
to investigate the continuity of this function at zero?. The
answer is obviously not, because zero is not in the
domain. Modify slightly the definition by considering the
function
and the point c=0. Does it make sense
to investigate the continuity of this function at zero?. The
answer is obviously not, because zero is not in the
domain. Modify slightly the definition by considering the
function 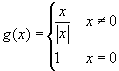 . The question of
continuity in zero now makes sense, but the function is not
continuous, as
. The question of
continuity in zero now makes sense, but the function is not
continuous, as 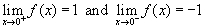 , so that
the limit does not exist. Going a step further we could
consider a still slightly different situation:
, so that
the limit does not exist. Going a step further we could
consider a still slightly different situation: 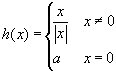 . Now the question may be: can we find a value
a for which the function is continuous? The answer
is again negative, because the limit of the function
can't exist, no matter what a is.
. Now the question may be: can we find a value
a for which the function is continuous? The answer
is again negative, because the limit of the function
can't exist, no matter what a is.
-
Example 3: Consider the function:
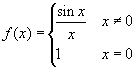 . Now, as we know from a fundamental limit
already discussed, the function is continuous in zero.
Observe that if we change the value f(0) to
something different the function is no more continuous: we
have chosen f(0)=1 just to make the function
continuous.
. Now, as we know from a fundamental limit
already discussed, the function is continuous in zero.
Observe that if we change the value f(0) to
something different the function is no more continuous: we
have chosen f(0)=1 just to make the function
continuous.
-
Example 4: Consider the function
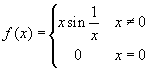 . The function is continuous at zero: it is the
product of x, that tends to zero, times a bounded
function (see algebraic
rules), so
. The function is continuous at zero: it is the
product of x, that tends to zero, times a bounded
function (see algebraic
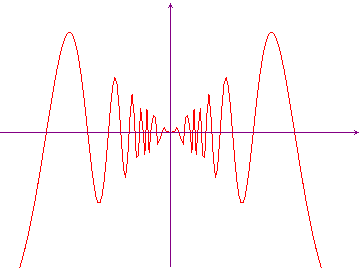
rules), so 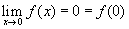 . We may
ask: can we draw the graph of this function without lifting
our pencil from the paper? To answer this question we must
before all calculate the length of the curve in the interval,
say, [-1,1]: this length is infinite! So the rough definition
given at the top of this page does not work in this case: the
concept of continuity is not so obvious. See the graph in the
picture here below.
. We may
ask: can we draw the graph of this function without lifting
our pencil from the paper? To answer this question we must
before all calculate the length of the curve in the interval,
say, [-1,1]: this length is infinite! So the rough definition
given at the top of this page does not work in this case: the
concept of continuity is not so obvious. See the graph in the
picture here below.
-
Example 5: Consider the function
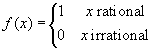 . This function, often called
Dirichlet's function, is continuous at no point
in the real line: it's a very strange function! Its graph
can only be imagined, and no computer display can visualize
it, as the values of f jump unceasingly between 0
and 1.
. This function, often called
Dirichlet's function, is continuous at no point
in the real line: it's a very strange function! Its graph
can only be imagined, and no computer display can visualize
it, as the values of f jump unceasingly between 0
and 1.
-
Example 6: Consider the function
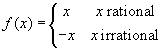 . This is a modification of the previous one:
it jumps unceasingly between the two bisectors y=x
and y=-x. It is continuous only at zero (!) and
obviously the problem of graphing it without lifting the
pencil from the paper makes no sense, even if we consider
only a small neighbourhood of zero.
. This is a modification of the previous one:
it jumps unceasingly between the two bisectors y=x
and y=-x. It is continuous only at zero (!) and
obviously the problem of graphing it without lifting the
pencil from the paper makes no sense, even if we consider
only a small neighbourhood of zero.
Facts about continuous functions
As continuity is defined in terms of limits, it's obvious that sums, products, quotients and compositions of continuous functions are continuous.