Rules of limits
How can one calculate limits? It's important to point out that this problem is, in general, very difficult and in many cases special investigation is required for each case. However in the simple situations with which we'll be involved, some simple rules can be used. We'll summarize here the most important ones.
Use of known properties of elementary functions
There is not a universal agreement on what elementary functions are. We mean here polynomials, radicals and in general powers with real exponents, trigonometric functions, logarithms, exponentials.
The main result as far these functions are concerned is that, if
c is a point in the domain, we have ![]() . As we shall see this is a property of what we
call continuous functions. So the problem of finding
limits for these functions as x tends to a point in the
domain is trivial.
. As we shall see this is a property of what we
call continuous functions. So the problem of finding
limits for these functions as x tends to a point in the
domain is trivial.
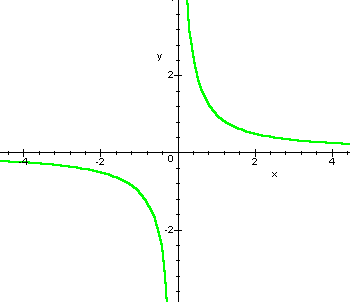
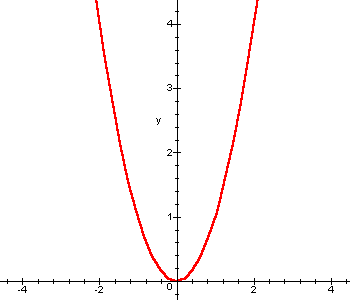
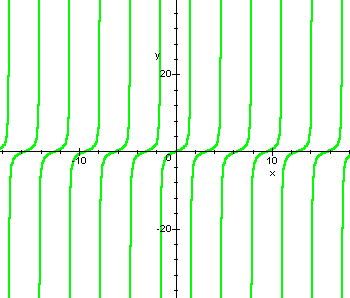
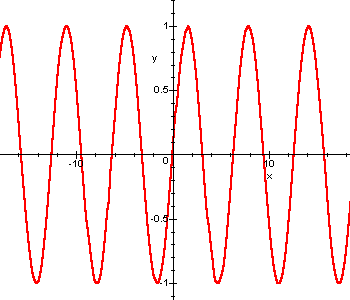
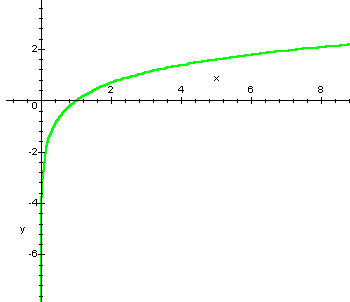
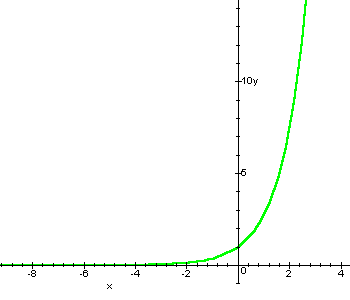
Other results concerning elementary functions can be deduced by simple observation of the graphs.
![]()
![]()
![]()
![]()
![]()
![]()
Algebraic rules
Suppose we have two functions ![]() ,
and a real number c, that is an accumulation point for
both D and E. Suppose also that
,
and a real number c, that is an accumulation point for
both D and E. Suppose also that ![]() (+∞ or -∞ are allowed for
c, l, m). In this case it is possible to calculate the
limits of the sum, the product and the quotient of the two
functions, simply by summing, multiplying, dividing the two
limits l and m, provided the operations
between l and m are defined in the extended
real line.
(+∞ or -∞ are allowed for
c, l, m). In this case it is possible to calculate the
limits of the sum, the product and the quotient of the two
functions, simply by summing, multiplying, dividing the two
limits l and m, provided the operations
between l and m are defined in the extended
real line.
The only cases where the operations are not defined can be summarized as follows:
![]()
- The sum of two opposite infinites: (+∞)+(-∞), (-∞)+(+∞), (+∞)-(+∞), (-∞)-(-∞).
- The product of zero by an infinite: 0·(∞).
-
The quotient of two zeros or two infinites:
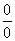 and
and 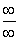 .
.
These cases require special attention. Usually they are called indeterminate forms, but we don't like this expression: there is nothing indeterminate here! The only problem is that the calculation of the limit is, in these cases, not easy. It would be better to call them difficult forms!.
Important extensions of the algebraic rules are:
- If f tends to infinity and g has no limit but is bounded between two real numbers a and b, then f+g tends to infinity.
- If f tends to zero and g has no limit but is bounded between two real numbers a and b, then fg tends to zero.
- If f tends to infinity and g has no limit but is always greater than a positive number a or lesser than a negative number b, then fg tends to infinity, with the correct sign.
- Similar rules apply to the quotient: it is sufficient to reduce the quotient to a multiplication.
Examples
![]() ,
, ![]() ,
, ![]() .
Observe that
.
Observe that ![]() , as you can deduce using
the graph of the function.
, as you can deduce using
the graph of the function.
Important observation
Sometimes functions of the form f(x)g(x) are used. They are best treated, not only as far as limits are concerned, if we observe that, as a consequence of the definition of natural logarithm, we have:
![]() .
.
Using this formula we can write a power were both the bases and the exponent are variables, as a power were only the exponent is variable. This proves very useful every time we want to study functions of this kind.
Observe that this formula highlights the fact that in the function f(x)g(x), the bases, f(x), must be strictly positive.
The sandwich or squeezing principle
Suppose that we have three functions f, g, h, and a
real number c that is an accumulation point for the
domains of each function. The functions verify the following:
f(x) ≤ g(x) ≤ h(x),
for every x, except possibly c, in a
neighbourhood of c. Suppose furthermore that ![]() . In this case we also have:
. In this case we also have: ![]() .
.
The proof of this theorem is very easy. The following picture is self evident: if the green graph is compelled between the yellow and blue ones that pass through (0,1), it must also pass through the same point.
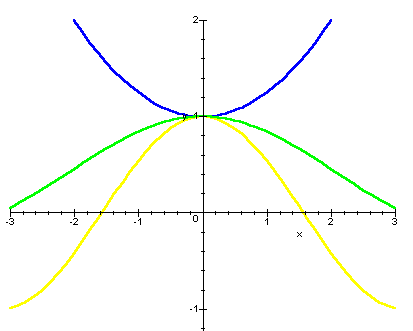
This theorem is known in Italy as "Teorema dei due carabinieri"
Two important limits
The sandwich theorem, is immediately used to prove that:
![]()
by far the most important limit in elementary analysis. You can also seee a graphical proof.
Another very important limit in elementary analysis is the following:
![]()
whose proof is omitted.