Rettificazioni e quadrature
Il problema che vogliamo affrontare in questa pagina è composto da due parti:
-
data una linea piana di lunghezza finita, costruire, con riga e compasso, un segmento avente la stessa lunghezza (rettificazione di una linea);
-
data una regione piana di area finita, costruire, con riga e compasso, un quadrato avente la stessa area della regione (quadratura di una regione piana).
Tratteremo questo problema solo a livello elementare, per cui supporremo che le linee e le regioni in esame siano prive di patologie strane. In particolare ci occuperemo di regioni con contorno costituito da segmenti o archi di cerchio, in numero finito. In molti casi ci limiteremo a semplici commenti alle figure proposte. Segnaliamo altresì che le costruzioni proposte non sono le uniche possibili e invitiamo lo studente a cercarne altre, magari più efficienti.
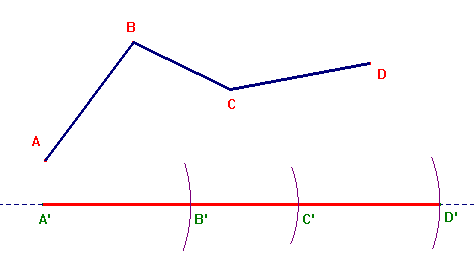
Problema 1: Data una spezzata con un numero finito di lati costruire un segmento avente la stessa lunghezza.
Si tratta di un problema di banale soluzione: basta riportare ciascun lato della spezzata su una retta come indicato nella figura sotto. Questa costruzione permette di rettificare il contorno di un qualunque poligono.
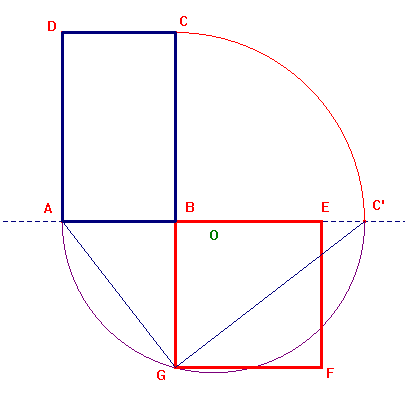
Problema 2: Dato un rettangolo ABCD costruire un quadrato ad esso equivalente.
Si tratta semplicemente di applicare il teorema di Euclide: riportato BC in BC' e costruito il semicerchio di diametro AC' (e centro O), il quadrato BEFG, costruito sull'altezza relativa all'ipotenusa del triangolo rettangolo AGC', è il quadrato cercato.
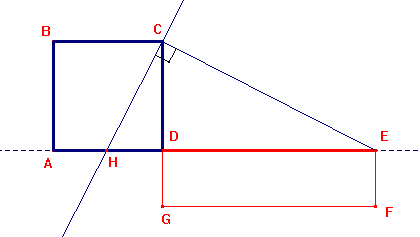
Problema 3: Dato un quadrato ABCD costruire un rettangolo ad esso equivalente e avente un lato assegnato.
Si tratta del problema inverso del precedente. Basta riportare il lato assegnato sul prolungamento di AD, in DE, e di costruire il triangolo rettangolo ECH. Il quadrato dato è quello costruito sull'altezza relativa all'ipotenusa, per cui il rettangolo richiesto avrà dimensioni HD e DE. Nella figura qui sotto HD è riportato in DG.
Problema 4: Dato un triangolo ABC costruire un rettangolo ad esso equivalente.
Si esamini solo la figura qui sotto, tenendo conto che M è il punto medio di AB.
Dunque ogni poligonale (con un numero finito di lati) è rettificabile elementarmente e ogni regione chiusa a contorno poligonale (con un numero finito di lati) è quadrabile elementarmente.
Si pone ora il problema di risolvere lo stesso problema per altre figure, in particolare per la circonferenza e il cerchio. Il problema della quadratura del cerchio o quello, equivalente, della rettificazione della circonferenza è di quelli che hanno più a lungo angustiato i matematici e solo Lindemann nel 1882 risolse definitivamente il problema in un celebre articolo dal titolo Über die Zahl π, pubblicato sui Matematische Annalen. Questo articolo è noto universalmente come la dimostrazione della trascendenza di π, e la conclusione è che la quadratura del cerchio è impossibile con riga e compasso.
Questo non significa affatto che sia impossibile quadrare, con riga e compasso figure dal contorno curvilineo. Ricordiamo qui solo i due casi più famosi: il segmento di parabola (problema risolto da Archimede) e le lunule di Ippocrate.
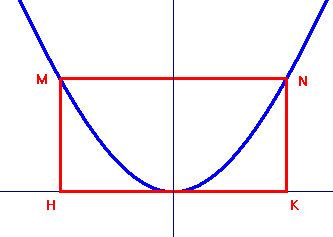
Per quanto riguarda il segmento di parabola Archimede ha provato che esso è equivalente ai 2/3 del parallelogramma costruito come in figura. Il risultato rimane valido anche se la corda MN non è perpendicolare all'asse, purché HK sia tangente alla parabola.
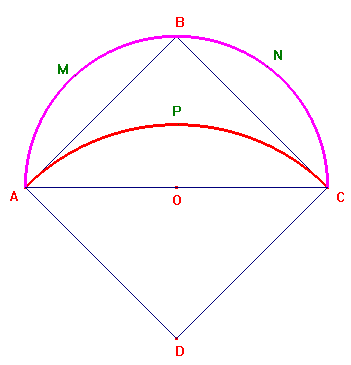
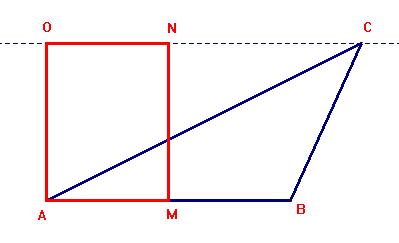
Per quanto riguarda le lunule di Ippocrate consideriamo il
quadrato ABCD e i due archi di cerchio ABC e APC, aventi centro
rispettivamente in O e D. La regione tra essi compresa è
una lunula. L'area della lunula è
determinabile con un calcolo elementare, osservando che si
può ottenere per differenza tra il semicerchio OABC e il
segmento circolare OAPC, il quale ultimo è la differenza
tra il quarto di cerchio DAPC e il triangolo ADC. Si ottiene
facilmente: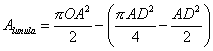 
, ovvero, tenendo conto che
AD2=2OA2 (per Pitagora), 
, che è come dire che l'area della lunula
è metà del quadrato. Anche se questo non è
il ragionamento fatto da Ippocrate, si conclude subito che la
lunula è quadrabile. La quadrabilità di questa e
altre lunule fece nascere nei matematici la speranza che anche
il cerchio fosse quadrabile, cosa che, come abbiamo visto, non
è possibile.
