Le funzioni iperboliche
In molte applicazioni hanno un ruolo particolarmente importante alcune speciali combinazioni della funzione esponenziale. Si tratta delle seguenti due funzioni:
-
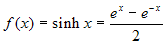 (funzione
seno iperbolico)
(funzione
seno iperbolico)
-
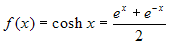 (funzione
coseno iperbolico)
(funzione
coseno iperbolico)
Le proprietà principali di cui godono sono indicate di seguito e possono essere provate come utile esercizio sulla funzione esponenziale.
-
cosh2x - sinh2x = 1 (questo è il motivo del loro nome: l'equazione x2-y2=1 è quella di un'iperbole equilatera).
-
sinh(-x) = -sinhx
-
cosh(-x) = coshx
-
sinh(x+y) = sinhxcoshy + coshxsinhy
-
cosh(x+y) = coshxcoshy + sinhxsinhy
-
(Dsinh)(x) = coshx
-
(Dcosh)(x) = sinhx
I grafici di queste funzioni sono riportati qui sotto.
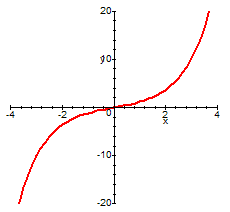
funzione seno iperbolico
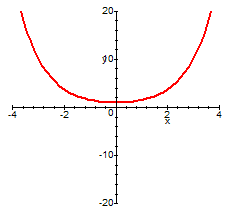
funzione coseno iperbolico
Si deduce immediatamente da questi grafici che la funzione seno iperbolico è invertibile, mentre la funzione coseno iperbolico è invertibile se si considera una sua restrizione, per esempio, ai reali positivi: queste inverse si chiamano, rispettivamente, settoresenoiperbolico (settsinh(x)) e settorecosenoiperbolico (settcosh(x)).
Naturalmente, in analogia con quanto si fa con le funzioni trigonometriche, si possono considerare anche altre funzioni (tangente iperbolica, cotangente iperbolica, ecc.), ma esse sono molto meno importanti nelle applicazioni.