L'algoritmo per la radice quadrata
L'algoritmo per il calcolo a mano della radice quadrata è una di quelle cose che avevamo proprio messo nel dimenticatoio: si tratta di un metodo piuttosto macchinoso, che ci è stato insegnato come una regoletta da imparare a memoria e da applicare solo ed esclusivamente nel compito di matematica appositamente preparato dall'insegnante per vedere se lo avevamo studiato. L'occasione per riprenderla in mano ci è fornita da nostro figlio Daniele che l'ha studiata in questi giorni.
Ai nostri tempi, dimenticato in fretta questo metodo, calcolavamo le radici quadrate utilizzando le apposite tavole. I nostri figli sono più fortunati e hanno a disposizione simpatici giochini, chiamati calcolatrici tascabili, che riescono a fare i conti richiesti, con un elevato numero di "cifre dopo la virgola", in un battibaleno. Abbiamo voluto scrivere questa pagina non per riproporre l'odiato algoritmo, studiato tanti anni fa, quanto piuttosto per far vedere che, in realtà, quell'algoritmo non é un'astrusa regoletta da imparare a memoria, ma un metodo efficiente e facile da applicare e soprattutto da ricordare se si utilizza un po' di fantasia. La tecnica proposta in questa pagina, seppure poco importante a scopi pratici, è invece, secondo noi, molto istruttiva per le varie implicazioni connesse. Per dovere di cronaca e per un utile confronto con quanto diremo, riportiamo un esempio di applicazione dell'algoritmo classico.
La prima cosa da fare è determinare di quante cifre sarà composta la radice quadrata di un numero. Per fare questo osserviamo che:
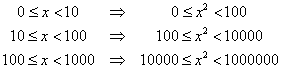
ovvero che, se un numero ha 1 cifra il quadrato ne ha 1 o 2, se ha due cifre, il quadrato ne ha 3 o 4, se ha 3 cifre, il quadrato ne ha 5 o 6. Letto in senso contrario ciò significa che se un numero ha 1 o 2 cifre la radice quadrata ne ha 1 (ovviamente nella sua parte intera, perché il numero potrebbe non essere un quadrato perfetto), se ha 3 o 4 cifre la radice quadrata ne ha 2, ..., se ha 11 o 12 cifre, la radice quadrata ne ha 6, ecc.
Se consideriamo il numero 7835473 (lo stesso che abbiamo usato
nell'esempio d'uso della regoletta mnemonica), che ha 7
cifre, potremo concludere che la parte intera della sua radice
ne avrà 4. Possiamo scrivere questo numero come
abcd, cioè possiamo scrivere 
. Si tratta di trovare
le cifre a, b, c, d (cifre
delle migliaia, delle centinaia, delle decine, delle
unità), mentre non siamo interessati, in questa fase,
alle cifre dopo la virgola. La cosa che ci interessa è
che il quadrato di abcd dovrà essere il massimo
quadrato perfetto minore od uguale al numero 7835473. Possiamo
rappresentare graficamente il quadrato del numero abcd,
come un quadrato di lato abcd scomposto, come nella
figura qui sotto (che non è in scala!), in quadrati e
rettangoli. Determineremo una ad una le cifre a,
b, c, d, ragionando sulla figura:
ritroveremo, come è ovvio, il risultato già
trovato con la regoletta mnemonica, ma in più ci
renderemo anche conto del perché di quella regoletta e,
se per caso ci trovassimo nel mezzo del deserto e la nostra
sopravvivenza dovesse dipendere solo dalla capacità di
calcolare la radice quadrata di un numero di 15 cifre, potremmo
cercare di ricostruire quella regola (di norma è
più facile memorizzare le immagini che non aride regole).
Per trovare b osserviamo che in quest'area rimasta esso contribuisce a formare due rettangoli di base 2000 e altezza bx100 e un quadrato di lato bx100. La somma delle aree di queste tre parti deve essere minore di 3835473.
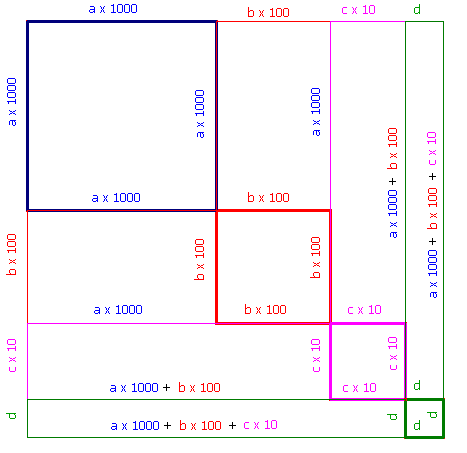
Per una prima stima grossolana di b trascuriamo il quadrato e consideriamo solo i due rettangoli. Dividiamo 3835473 per 4000 (il doppio di 2000, perché è la somma delle basi dei due rettangoli: ecco perché nella regoletta uno dei passaggi richiede il raddoppio della parte di radice trovata fino a quel momento): otteniamo circa 958. (Per inciso osserviamo che questa stima grossolana si può fare dividendo 38, cioè le prime due cifre di 383, per 4, cioè il doppio di 2: è esattamente questo che ci imponeva la regoletta pratica). Ciò significa che b potrebbe essere 9 (958 è 9,58x100), ma potrebbe anche essere meno, perché, per ora, abbiamo trascurato il quadrato di lato bx100. Non ci resta altro che provare. Se supponiamo che b sia nove, l'area complessiva (2 rettangoli più un quadrato) diventa 2x2000x900+900x900=4410000, decisamente troppo. Se supponiamo che b sia otto, l'area complessiva (2 rettangoli più un quadrato) diventa 2x2000x800+800x800=3840000, ancora un po' troppo, ma non molto: sette andrà sicuramente bene. Difatti 2x2000x700+700x700=3290000.
Per trovare c ragioniamo nello stesso modo: l'area rimasta è minore di 3835473-3290000=545473, e contiene due rettangoli di base 2700 e altezza cx10, più un quadrato di lato cx10. Con la stessa tecnica di prima (dividere 545473 per il doppio di 2700 e provare) si trova che c=9. Infine d si trova allo stesso modo ragionando sui due rettangoli di base 2790 e altezza d e sul quadrato di lato d. Si trova d=9. Se ne deduce che la radice cercata è 2799 e che rimane un residuo di 1072, non rappresentato nella figura di sopra, che costituisce la differenza tra il numero dato e il quadrato perfetto immediatamente precedente.
Puoi caricare un programma in Javascript per eseguire il calcolo della radice con il metodo tradizionale. Il programma è stato realizzato da Giovanni Pizzi, classe IVB del Liceo Scientifico Grigoletti di Pordenone, A.S. 2001/2002. L'utilizzo di questo programma ha come unica limitazione i soliti problemi di overflow di Javascript con gli interi troppo grandi (che qui possono comparire nei resti).