Il problema del periodo nove nei decimali
Questa pagina ha, volutamente, un linguaggio elementare ed intuitivo ed è stata pensata e realizzata in collaborazione con i nostri figli che frequentano la prima e seconda classe di scuola media inferiore.
Il problema che vogliamo esaminare è il seguente: perché 0,99999... è uguale ad uno?
Da un punto di vista teorico naturalmente non c'è alcuna difficoltà, basta usare la frazione generatrice o, meglio, il seguente semplice ragionamento: se x=0,999..., allora 10x=9,999.... Sottraendo la prima dalla seconda si trova (tutte le cifre dopo la virgola scompaiono nella sottrazione) 9x=9,000..., da cui, banalmente x=1.
Questo calcolo non fornisce una giustificazione intuitiva del risultato. Il problema non è banale perché, come si potrebbe dimostrare, nessuna divisione tra numeri interi può produrre decimali con periodo nove.
Per i puristi, cioè i veri matematici che non vogliono giustificazioni dal sapore metafisico, il modo corretto di risolvere questo "enigma" è chiaramente quello di affrontare in dettaglio il vero problema soggiacente, cioè: cosa è 0,9999...? Noi qui ci vogliamo limitare ad un semplice gioco e proponiamo alcune "giustificazioni" intuitive di questo risultato.
Prima "giustificazione"
Per capire il discorso che segue bisogna sapere che ![]() , ma questo fatto non crea problemi, perché basta
eseguire la divisione 1:9. Analizziamo allora le due serie di
numeri seguenti
, ma questo fatto non crea problemi, perché basta
eseguire la divisione 1:9. Analizziamo allora le due serie di
numeri seguenti
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Il punto di partenza delle due serie è lo stesso. Nella
prima i numeri aumentano di una quantità costantemente
uguale a 0,1 (1/10), nella seconda fila di una quantità
uguale a ![]() (1/9). Ora un nono è
leggermente più grande di un decimo, esattamente si ha:
(1/9). Ora un nono è
leggermente più grande di un decimo, esattamente si ha:
![]() . Nella prima serie ci sono undici numeri e dieci
incrementi, che in totale fanno uno, che è il valore
finale. Nella seconda serie ci sono dieci numeri e nove
incrementi che in totale fanno:
. Nella prima serie ci sono undici numeri e dieci
incrementi, che in totale fanno uno, che è il valore
finale. Nella seconda serie ci sono dieci numeri e nove
incrementi che in totale fanno: ![]() , per
cui il risultato finale è sempre lo stesso.
, per
cui il risultato finale è sempre lo stesso.
Seconda "giustificazione"
Si tratta sostanzialmente di un modo diverso di leggere il precedente calcolo. I numeri della seconda serie della tabella precedente aumentano progressivamente di 1/9, per cui si ottiene la tabella seguente:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Siccome poi 9/9 è uno...
Terza "giustificazione"
Consideriamo le seguenti sottrazioni:
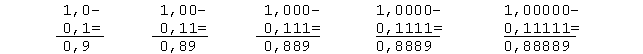
La successione di questi calcoli prova che, se continuiamo a
prendere, nel minuendo e nel sottraendo, un numero crescente di
zero e di uno, alla fine otterremo:
1,000000...-0,111111...=0,888888.... Questo risultato è
naturalmente corretto perché equivale a ![]() .
Proseguendo con questo criterio non dovrebbe essere difficile
capire la costruzione di questa tabella di sottrazioni:
.
Proseguendo con questo criterio non dovrebbe essere difficile
capire la costruzione di questa tabella di sottrazioni:
| 1,000000... - 0,111111... = 0,888888... |
| 1,000000... - 0,222222... = 0,777777... |
| 1,000000... - 0,333333... = 0,666666... |
| 1,000000... - 0,444444... = 0,555555... |
| 1,000000... - 0,555555... = 0,444444... |
| 1,000000... - 0,666666... = 0,333333... |
| 1,000000... - 0,777777... = 0,222222... |
| 1,000000... - 0,888888... = 0,111111... |
| 1,000000... - 0,999999... = 0,000000... |
Questa tabella prova il risultato cercato, perché nell'ultima riga i due numeri del primo membro devono essere uguali, avendo per differenza zero, e anche perché ciascuna riga della tabella può essere letta, portando il sottraendo a secondo membro, come 1,000000...=0,999999...!
Detto in altri termini si ha: ![]() .
.
Quarta "giustificazione"
Si può procedere ad una diversa giustificazione con il
seguente ragionamento: ![]() , il quale nasconde, in
realtà, un calcolo coinvolgente le serie geometriche (in
questo caso di ragione 1/10).
, il quale nasconde, in
realtà, un calcolo coinvolgente le serie geometriche (in
questo caso di ragione 1/10).
Quinta "giustificazione"
Questo calcolo è sostanzialmente preso da
H.M.Enzensberger, Il Mago dei numeri,
Einaudi, Torino 1997. E' immediato che ![]() (basta fare la divisione...). Ora deve essere,
necessariamente,
(basta fare la divisione...). Ora deve essere,
necessariamente, ![]() . Proviamo a scrivere
quest'ultima uguaglianza in un altro modo. Per fare questo
consideriamo le seguenti moltiplicazioni:
. Proviamo a scrivere
quest'ultima uguaglianza in un altro modo. Per fare questo
consideriamo le seguenti moltiplicazioni:
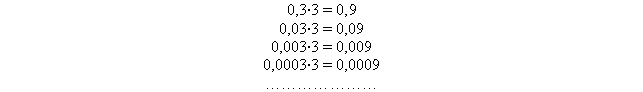
Se sommiamo tutti i primi membri, raccogliendo il 3 a fattor comune, e tutti i secondi membri otteniamo: (0,3+0,03+0,003+0,0003+...)×3=(0,3333...)×3=0,9999..., cioè, di nuovo, 1=0,9999...! Naturalmente si poteva anche fare, direttamente, 1=0,3333...×3=0,9999..., ma il calcolo precedente ci pare faccia emergere meglio le difficoltà insite in questo problema.
Sesta "giustificazione"
In realtà, gira e volta, si tratta solo di riscrivere la stessa cosa in altri modi: questo ci è stato suggerito da nostro figlio Alberto che fa la seconda media. Se proviamo a sommare, con la usuale regola, 0,9999... con 0,1111... otteniamo:
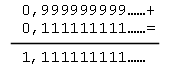
Basta osservare che la somma si esegue cominciando dall'estrema destra e quindi l'ultima addizione darebbe zero con riporto di uno: successivamente i riporti (sempre di uno) influenzano tutte le cifre successive...Ora questa somma è la stessa che si ottiene se si fa 1,0000...+0,1111..., e quindi...
Settima "giustificazione"
Questo calcolo ci è venuto in mente provando a spiegare, a livello elementare, il problema di Achille e la tartaruga. E' abbastanza semplice riuscire ad intuire che, se prendiamo un segmento lungo 1/2 (in qualunque unità...), e gli affianchiamo un secondo segmento lungo 1/4, poi uno lungo 1/8, e così via, alla fine, dopo aver aggiunto infiniti segmenti, ne otterremo uno lungo esattamente 1. (E' per questo che Achille, se ha velocità doppia della tartaruga, la può raggiungere in un tempo finito, ma forse il problema di Zenone è un tantino più complesso!). Il disegno qui sotto rende evidente questo fatto.
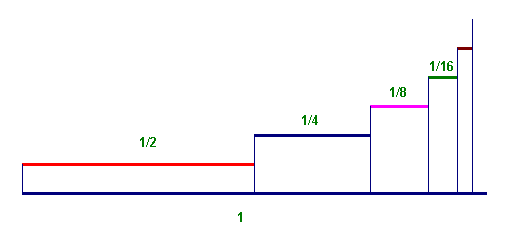
In formule si può scrivere: ![]() . Se
scriviamo questo calcolo in termini di decimali otteniamo:
. Se
scriviamo questo calcolo in termini di decimali otteniamo: ![]() . Basta
una semplice calcolatrice per "provare" che
il primo membro di questa uguaglianza fa, appunto, 0.9999999...
. Basta
una semplice calcolatrice per "provare" che
il primo membro di questa uguaglianza fa, appunto, 0.9999999...
Sono bene accetti altri modi di "spiegare" questo fatto in apparenza strano!