Definizioni
Coppia ordinata
Il concetto di coppia ordinata è uno di quelli di più largo consumo in matematica. Intuitivamente, dati due elementi a e b non necessariamente distinti, la coppia (a,b) consiste degli elementi "presi in questo ordine", cioè con a "primo elemento" e b "secondo elemento". Per una definizione rigorosa occorrerebbe avere già la nozione di ordine, che invece è sempre successiva a quella di coppia ordinata. Si può ovviare a questo inconveniente con la definizione seguente:
(a,b) = {a,{a,b}}
E' molto importante osservare che (a,b) è diverso da {a,b}. Se in particolare a e b sono uguali l'insieme {a,b} coincide con l'insieme {a}, mentre (a,b) coincide, secondo la definizione che abbiamo dato, con {a,{a}}, da cui emerge chiaramente la differenza tra il primo e il secondo elemento della coppia.
Il risultato più importante relativamente alle coppie ordinate è espresso dal seguente:
Teorema: Se a, b, c, d sono elementi,
![]() .
.
La dimostrazione è abbastanza noiosa e lunga (si tratta di una dimostrazione fatta in un momento in cui gli "attrezzi" a disposizione sono ancora molto pochi) ed esula dagli scopi di questa breve trattazione. In ogni caso nel concetto di coppia ordinata (e poi di terna, quaterna, ecc.) quello che conta è proprio il risultato di questo teorema. Una immagine che ci è particolarmente piaciuta e che rende evidente il significato di coppia ordinata è presa da una dispensa di Gianluca Gorni (http://www.dimi.uniud.it/~gorni/):
![]() Una
coppia ordinata è un chip di memoria "( ,
)" che imbraca due elementi in modo da restituirli, a
richiesta, nell'ordine in cui sono stati inseriti. La coppia
non ordinata "{ , }", invece, li mescola
irrimediabilmente.
Una
coppia ordinata è un chip di memoria "( ,
)" che imbraca due elementi in modo da restituirli, a
richiesta, nell'ordine in cui sono stati inseriti. La coppia
non ordinata "{ , }", invece, li mescola
irrimediabilmente.
Prodotto cartesiano
Dati due insiemi A e B si chiama loro
prodotto cartesiano l'insieme, indicato con
A×B costituito da tutte e sole le coppie
ordinate (a,b), in cui a![]() A e
b
A e
b![]() B.
B.
A proposito del prodotto cartesiano valgono i seguenti risultati:
-
Per ogni insieme A si ha A×
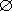 =
= 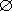 ×A =
×A = 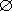 .
.
-
Se A e B sono insiemi non vuoti si ha
A×B = B×A
 A = B.
A = B.
La rappresentazione grafica del prodotto cartesiano di due insiemi si può fare in vari modi. Nel caso di prodotti tra insiemi finiti o tra sottoinsiemi di R la rappresentazione più comune è quella che utilizza un sistema di coordinate cartesiane nel piano, in cui si stabilisce una corrispondenza biunivoca tra punti di opportuni sottoinsiemi del piano e il prodotto cartesiano A×B.
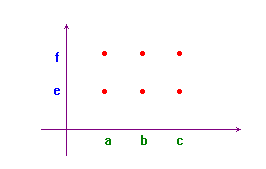
Se per esempio A = {a, b, c} e B = {e, f}, si può rappresentare il prodotto A×B come nella figura qui sotto. Si noti che l'unità di misura e l'ordine sugli insiemi dati non hanno alcun interesse.
Relazioni tra insiemi
Dati due insiemi A e B si chiama relazione
(binaria) tra A e B un qualunque sottoinsieme, ![]() , del prodotto cartesiano A
×B. Le relazioni tra A e A
vengono dette relazioni in A.
, del prodotto cartesiano A
×B. Le relazioni tra A e A
vengono dette relazioni in A.
Se ![]() è una relazione tra A e B, invece di
scrivere (a,b)
è una relazione tra A e B, invece di
scrivere (a,b) ![]()
![]() , si usa scrivere a
, si usa scrivere a![]() b e si legge "a è
in relazione con b".
b e si legge "a è
in relazione con b".
La definizione data comprende tutti i possibili sottoinsiemi del prodotto cartesiano di due insiemi. Nella pratica non tutte le relazioni hanno importanza, ma solo quelle che verificano alcune proprietà che le rendono più "dignitose". Per le relazioni di uso più comune si usano speciali simboli, come ≈, ≤, ecc.
La rappresentazione si può fare con un grafico cartesiano, come sopra, o con una "rappresentazione sagittale", particolarmente utilizzata per insiemi finiti.
Se per esempio A = {a, b, c}, B
= {e, f}, e ![]() =
{(a,f), (c,f), (c,e)}, si può
usare il diagramma qui sotto.
=
{(a,f), (c,f), (c,e)}, si può
usare il diagramma qui sotto.
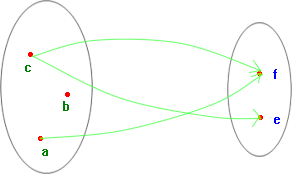
L'insieme A viene detto dominio della relazione, l'insieme B viene detto codominio.
Esempi.
-
La relazione in R2:
x
 y
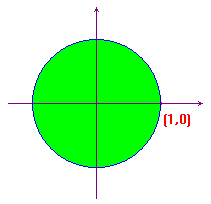
y  x2+y2<1 ha come grafico il
cerchio di centro l'origine e raggio 1, privato del
bordo.
x2+y2<1 ha come grafico il
cerchio di centro l'origine e raggio 1, privato del
bordo.
-
La relazione in R2:
x
 y
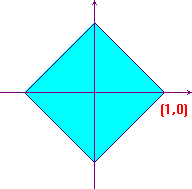
y  |x|+|y|<1 ha come grafico il quadrato di centro
l'origine disegnato nella figura qui sotto (privato del
bordo).
|x|+|y|<1 ha come grafico il quadrato di centro
l'origine disegnato nella figura qui sotto (privato del
bordo).
-
La relazione in R2:
x
 y
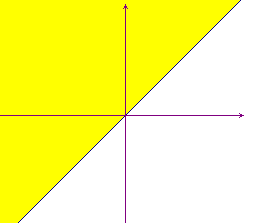
y  x<y ha come grafico il semipiano colorato nella
figura qui sotto (privato del bordo).
x<y ha come grafico il semipiano colorato nella
figura qui sotto (privato del bordo).
-
Nell'insieme di tutte le rette dello spazio la relazione che contiene tutte le coppie di rette parallele è detta "relazione di parallelismo". E' chiaro che non ha senso fare un grafico di una relazione di questo tipo. Si noti come, nella definizione di questa relazione, si ponga di solito piuttosto l'accento sul predicato in due variabili "x è parallela ad y", senza espliciti riferimenti a particolari sottoinsiemi del prodotto cartesiano dell'insieme delle rette per se stesso. Spesso, e in maniera equivalente, le relazioni sono definite come l'insieme delle coppie per cui un predicato in due variabili è vero.