Distribuzione
I numeri primi sono infiniti, ma come si distribuiscono all'interno dei numeri naturali? In sostanza è possibile stabilire quanti sono i numeri primi compresi tra 1 ed n, per ogni naturale n? Ovvero è possibile costruire una funzione analitica, che possiamo indicare con π(n), che fornisca questo valore?.
Che la cosa non sia semplice risulta da un esame delle tabelle di numeri primi. Si può osservare ad occhio che, all'aumentare di n, la "densità" di primi diminuisce, seppure in maniera non costante.
In realtà, pur di spostarsi molto in avanti, esistono intervalli di N di ampiezza arbitraria all'interno dei quali non ci sono primi. La cosa può essere provata con questo semplice ragionamento: sia n un naturale arbitrario e consideriamo il numero (n+1)!. Esso è divisibile per tutti i numeri da 1 ad n+1. Il numero (n+1)!+2 è sicuramente divisibile per 2, in quanto somma di due numeri divisibili per 2; il numero (n+1)!+3 è sicuramente divisibile per 3, in quanto somma di due numeri divisibili per 3; ...; il numero (n+1)!+(n+1) è sicuramente divisibile per (n+1), in quanto somma di due numeri divisibili per (n+1). Abbiamo così trovato un intervallo di n numeri consecutivi che non sono primi. Dato che n può essere arbitrario, si vede che esistono sicuramente, ma "molto in là", lunghissimi tratti senza primi.
Molti matematici hanno tentato di trovare formule per generare i numeri primi. Famosa è quella di Eulero: se si inseriscono i naturali da 0 a 39 in n2+n+41 si ottengono sempre numeri primi. Lo stesso Eulero però si rese conto della difficoltà di ottenere una formula semplice che generasse tutti i primi, tant'é che scrisse: «Ci sono alcuni misteri che la mente umana non penetrerà mai. Per convincersene non dobbiamo far altro che gettare un'occhiata alle tavole dei numeri primi. Ci accorgeremo che non vi regna né ordine né legge.»
Il primo ad occuparsi sistematicamente della distribuzione dei primi, spostando l'attenzione dalla ricerca di una formula che generasse i primi alla ricerca di una formula che calcolasse la distribuzione dei primi, fu (manco a dirlo!) Gauss, il quale ritenne, sulla base delle tavole a sua disposizione e che in gran parte aveva contribuito a costruire, che si potesse stabilire la seguente formula approssimata per il numero π(n) dei primi compresi tra 1 ed n:
.
Successivamente egli modificò la formula, ottenendo una
stima che si accordava decisamente decisamente meglio con i
valori noti: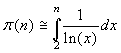 
.
Le due stime non sono in realtà molto diverse per valori
molto grandi di n. La prova non è immediata
perché la funzione che compare nella formula di sopra,
1/ln(x), non è elementarmente integrabile. Si
può però fare il seguente ragionamento: la
funzione x/f(x) ha come derivata la
funzione 1/ln(x) - 1/(ln(x))2, e il
secondo addendo è decisamente trascurabile, per
x grandi, rispetto al primo. Si ottiene allora (il
ragionamento meriterebbe qualche approfondimento, ma in ogni
caso funziona!):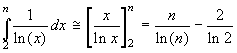 
, e il termine
costante è trascurabile per n grande.
Gauss addirittura congetturò che, al tendere di
n all'infinito, le funzioni π(n) e
n/ln(n) diventassero asintoticamente uguali,
in formule: 
. Questa congettura
fu provata da Jacques Hadamard e Charles de la
Vallée-Poussin, indipendentemente, nel 1896, e da allora
è nota come Teorema dei numeri primi. La
dimostrazione fu resa possibile grazie alle sensazionali
scoperte di Bernhard Riemann, allievo, almeno in parte, dello
stesso Gauss. Le idee di Riemann non sono semplici da esporre,
ma nella pagina successiva ne potete trovare almeno le idee essenziali. Chi volesse approfondimenti
ulteriori può fare riferimento al più volte citato
libro di M.du
Sautoy.