www.batmath.it

Una proprietà dei punti di accumulazione

La dimostrazione di questa proprietà è la seguente: 

1. Se 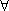U_c l'insieme U_c∩A contiene infiniti punti, è ovvio che U_c∩A\{c} è non vuoto.
2. Viceversa se 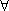U_c l'insieme U_c∩A\{c} è non vuoto (cioè U_c contine punti di A diversi da c), supponiamo per assurdo che U_c∩A contenga solo un numero finito di punti, e sia d, tra questi, il più vicino a c. Detta δ la distanza tra c e d, nel segmento ]c-δ,c+δ[, che è un intorno di c, non cade alcun punto di A diverso da c, contro l'ipotesi.

Questa dimostrazione è interessante più che per sé stessa, per il fatto che mette in luce l'importanza del " U_c"  nella definizione di punto di accumulazione.

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 07/12/2002 - ultimo aggiornamento il 01/09/2003