Disequazioni scomponibili in fattori
Una disequazione, ridotta in forma normale, in cui il primo membro sia scomponibile in fattori dei quali si possa determinare il segno, può essere agevolmente risolta utilizzando la regola dei segni. Può essere particolarmente utile la rappresentazione grafica che abbiamo proposto per rappresentare il segno delle funzioni. In questo modo si possono, in particolare, risolvere tutte le disequazioni che, ridotte in forma normale, abbiano al primo membro una funzione razionale, a patto di riuscire a scomporre i polinomi che compaiono al numeratore e al denominatore del primo membro in fattori al più di secondo grado. La cosa è sempre teoricamente possibile (teorema fondamentale dell'algebra), ma non è detto che le radici dei polinomi siano determinabili a partire dai coefficienti. Chiariremo il metodo con alcuni esempi.
Esempio 1. Risolvere la disequazione x3 - x2 - 2x > 0. Scomponendo in fattori si ottiene x(x+1)(x-2)>0. Si può agevolmente trovare il segno dei tre fattori e riportarlo in uno schema come il seguente:
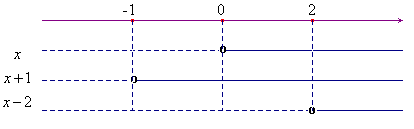
Da qui si deduce che la disequazione data è verificata
per -1 < x < 0 
x
> 2.
Esempio 2. Risolvere la disequazione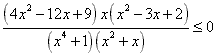 
. Troviamo preventivamente il dominio, andando
alla ricerca dei valori che annullano il denominatore: otteniamo
D = R\{-1,0}. Il primo membro risulta
già scomposto in fattori, dei quali si può trovare
agevolmente il segno. Lo abbiamo riportato nello schema
seguente, dividendo, solamente per motivi "estetici",
i fattori che compaiono al numeratore da quelli che compaiono al
denominatore: come è noto non vi è alcuna
differenza nel segno tra il prodotto e il quoziente di due
numeri.
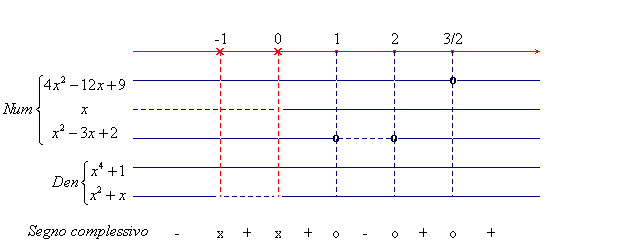
Abbiamo segnato con una "x", per maggiore sicurezza, i
valori esclusi dal dominio, già nella "linea di
riferimento": conviene sempre utilizzare questa tecnica, in
quanto in corrispondenza a questi valori non serve fare alcun
calcolo. Il segno complessivo si deduce subito con la regola dei
segni e da qui si conclude che la disequazione proposta ha il
seguente insieme di soluzioni: S = ]-∞,-1[ [1,2] {3/2}.
Si noti che nel trovare il segno del primo membro non ha avuto
alcuna influenza il verso della disequazione: in un problema
come questo il verso della disequazione va considerato
solo al termine dell'esercizio,
dopo aver trovato il segno del primo membro.