Esercizi riepilogativi sullo studio di funzione
Proponiamo in questa pagina qualche esempio comprendente tutte le tecniche e le strategie indicate per tracciare il grafico di una funzione.
Studiare la funzione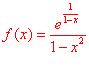 
, limitando
l'indagine alla derivata prima.
Dominio. 
.
Segno. Essendo il numeratore positivo, basta studiare il segno del denominatore: la funzione è positiva per valori interni all'intervallo [-1,1].
Continuità . Essendo la funzione composta di funzioni elementari è continua in tutto il dominio.
Limiti notevoli. Si ha: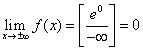 
; 
; 
, 
, 
.
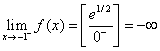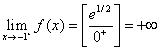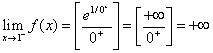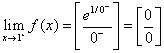Conviene scomporre il denominatore in 
,
osservare che il primo fattore tende a 2 e poi operare un cambio
di variabile 
. Se x tende ad 1 da
destra, t tenderà a -∞. Si ottiene di conseguenza:
.
Asintoti. I limiti precedenti ci permettono di affermare che non esistono asintoti obliqui, mentre la retta y=0 è asintoto orizzontale, e le due rette x=1 ed x=-1 sono asintoti verticali. Si può altresì concludere che i punti 1 e -1 sono entrambi discontinuità non eliminabili né a salto.
Derivata prima. Si ottiene facilmente: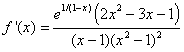 
. Il segno di questa funzione dipende unicamente
dal trinomio di secondo grado al numeratore e dal binomio di
primo grado al denominatore. Non è allora difficile
trarre concludere che la derivata è positiva in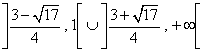 
, intervalli dove la funzione è crescente.
É interessante il calcolo dell'attacco per x
tendente ad 1 da destra. Conviene usare l'accorgimento
già usato per i limiti notevoli e scrivere la derivata
come 
. Il primo fattore tende a zero
(stessa tecnica di prima), il secondo è finito, dunque il
prodotto tende a zero: il grafico della funzione tende ad
avvicinarsi al punto (1,0), da destra, con una tangente
orizzontale.
Grafico. Riunendo i risultati trovati prima si può tracciare il grafico seguente:
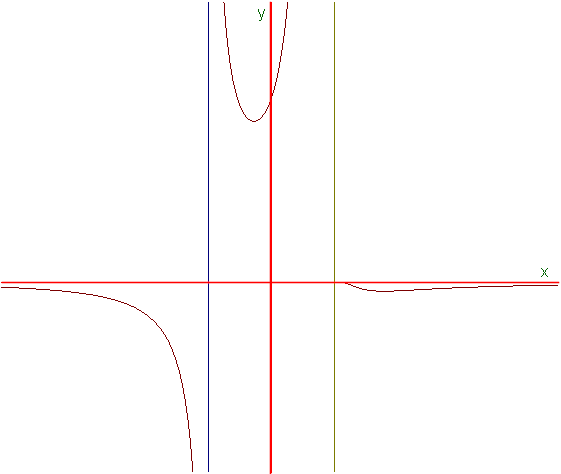
Studiare la funzione 
.
Dominio. La convenzione più seguita
è che la funzione radice cubica sia definita su tutto
R (anche se non valgono per essa le
proprietà formali: per esempio 
,
come si capisce subito se si osserva che il primo membro
può essere positivo o negativo, mentre il secondo
è sempre positivo). Dunque il dominio della funzione
è R. Si noti che se avessimo scritto
al posto di 
,
ci saremmo trovati in maggiori difficoltà interpretative,
in quanto le potenze con esponente razionale sono quasi sempre
considerate definite solo per basi positive: nel risolvere un
esercizio in cui compaiano situazioni di questo tipo consigliamo
sempre di consultare l'elenco dei simboli e delle
convenzioni del testo in uso.
Segno. La funzione ha, evidentemente, lo stesso segno di x. Questo comporta che è una funzione dispari e che dunque potremo limitarne lo studio solo ai reali positivi.
Limiti notevoli e asintoti. Si ha 
. Se ne deduce che la retta y=0 è un
asintoto orizzontale.
Derivata prima. Si ha 
.
Si conclude subito che la derivata è positiva (nei reali
positivi) per 
. É anche immediato
verificare che la derivata prima tende a +∞, sia a destra
che a sinistra, per cui la funzione ha un flesso verticale
ascendente in (0,0).
Derivata seconda. Si ha (se non ci credi usa
Derive!) 
. Il segno dipende solo (siamo
sui reali positivi!) dal polinomio di quarto grado del
numeratore, e si trova (equazioni biquadratiche) che è
positivo per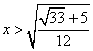 
. La funzione
sarà dunque concava tra 0 e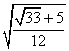 
,
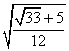convessa oltre . In corrispondenza di 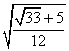si avrà un flesso.
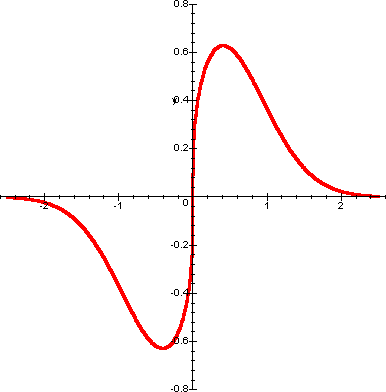
Grafico. Riassumendo i risultati trovati si trova il seguente grafico.
Osservazione sui software di calcolo automatico.
I più diffusi programmi del tipo citato per calcoli
matematici (Derive, Mathematica, Maple) non contengono la
funzione radice cubica tra quelle predefinite. Tale funzione va
sostituita con la potenza x1/3, con il problema
però che, anche secondo la convenzione che noi seguiamo
in questo sito, essa non risulta definita sui reali negativi.
Per ottenere il grafico sopra riportato abbiamo usato la
strategia di definire la funzione radice come 
. La tecnica è quella utilizzata per dare una
definizione della funzione radice cubica che non si presta ad
ambiguità e difficoltà legate all'uso delle
proprietà formali.