I corollari del teorema di Lagrange - dimostrazioni e considerazioni varie
Corollario 1. Se una funzione è derivabile con derivata nulla su un intervallo, allora è costante.
Basta considerare due punti d e x
dell'intervallo, di cui il primo fisso. Si ha 
, cioè
f(x) ha sempre lo stesso valore.
Si noti come l'inverso di questo corollario sia banale (la
derivata di una costante è zero), anche se la funzione
costante non è definita su un intervallo. Per questo
corollario è invece essenziale che la funzione sia
definita in un intervallo. Per esempio la funzione 
ha derivata nulla su R, ma non
è costante.
Corollario 2. Se due funzioni hanno la stessa derivata in un intervallo, esse differiscono per una costante.
Basta applicare il corollario precedente alla funzione differenza delle due funzioni date.
Questo corollario ha grande importanza per quanto riguarda il problema della ricerca delle primitive di una funzione, cioè delle funzioni F definite su un intervallo che abbiano come derivata una assegnata funzione f. Se il problema ha una soluzione F, tutte e sole le soluzioni sono del tipo F+k, con k costante arbitraria. Che F+k sia soluzione è banale, il corollario ci assicura che al variare di k, F+k fornisce tutte le soluzioni.
Corollario 3. Se una funzione ha derivata maggiore di zero in un intervallo, è strettamente crescente nell'intervallo.
Dati due punti m ed n
dell'intervallo si ha 
. Da qui segue f(m)>f(n) ovvero
f(m)<f(n) a seconda che m sia maggiore o
minore di n.
Naturalmente se la derivata è minore di zero, la funzione sarà strettamente decrescente. Data allora una funzione, se si riesce a calcolarne la derivata e a determinarne il segno si può concludere che in tutti gli intervalli dove la derivata è positiva la funzione è crescente, in tutti quelli dove è negativa la funzione è decrescente. Si usa abitualmente un grafico del tipo:
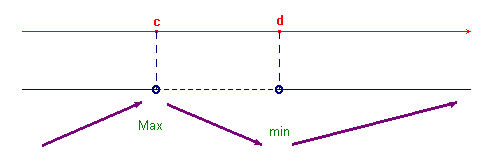
Le cose possono essere anche più complesse (funzioni che non sempre sono derivabili, funzioni che hanno derivate nulle su un intervallo,...), ma la situazione più comune è quella del grafico qui sopra.