Definizioni e prime proprietà
Come è noto a tutti (!) la tangente ad una circonferenza in un suo punto P può essere definita, equivalentemente, in uno dei seguenti modi:
- la perpendicolare al raggio condotta per P;
- l'unica retta passante per P che ha un solo punto in comune con la circonferenza;
- la posizione limite assunta dalla secante passante per P e un altro punto Q della circonferenza, quando Q tende a sovrapporsi a P.
La prima definizione non può essere chiaramente generalizzata ad altre curve (nemmeno alle coniche, parenti strette della circonferenza), che non possiedono un raggio. La seconda definizione può essere estesa alle coniche (con qualche attenzione nel caso della parabola, in modo da escludere rette parallele all'asse che incontrano la parabola in un solo punto senza esserle tangenti), ma non a curve più complesse. Basta pensare al grafico della funzione seno: è abbastanza intuitivo che la tangente nel punto di ascissa π/2 debba essere la retta y=1, ma questa retta tocca la curva in infiniti punti.
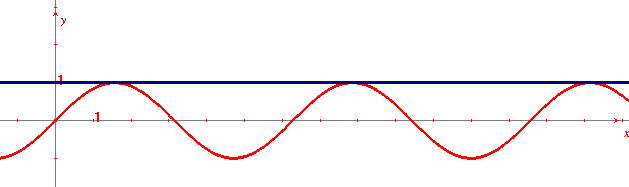
La terza definizione di tangente è invece quella che si presta ad una facile generalizzazione a curve complesse ed è quella comunemente adottata. Naturalmente per poterla formalizzare occorre una precisa definizione di che cosa si intenda con posizione limite. La cosa è abbastanza semplice nel caso delle curve grafico di funzioni di R in R e noi ci limiteremo a questo caso.
Definizione formale di derivata
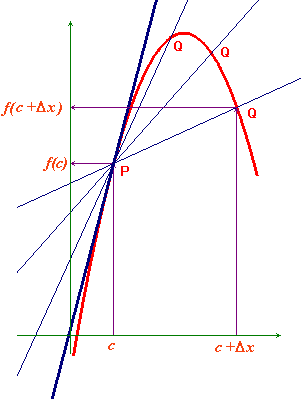
Considerata una funzione f che abbia come dominio un intervallo o un'unione di intervalli, un punto c del dominio e un incremento Δx tale che c+Δx stia ancora nel dominio, il coefficiente angolare della retta passante per i punti P e Q di figura (retta secante) si chiama rapporto incrementale di f relativo al punto c e all'incremento Δx:
Definizione: ![]() ,
nell'ipotesi che il limite esista finito.
,
nell'ipotesi che il limite esista finito.
Si noti che il limite si può anche scrivere nella forma,
equivalente, ![]() .
.
Se il limite è infinito o non esiste si dice che la funzione non è derivabile nel punto c.
Attenzione: la nomenclatura sopra utilizzata non è standard. Molti autori concordano nel chiamare derivata di una funzione anche il limite del rapporto incrementale nel caso che questo sia infinito. In questo caso però la definizione di funzione derivabile viene data (esattamente come abbiamo fatto noi) dicendo che una funzione è derivabile se ha derivata finita. Pur trattandosi di una scelta perfettamente legittima, ci pare illogico dire che una funzione può avere derivata senza essere derivabile. In ogni caso, trattandosi di convenzioni, è sufficiente conoscerle e regolarsi di conseguenza.
Se il punto c è estremo di un intervallo, naturalmente considereremo solo il limite destro o sinistro a seconda dei casi e parleremo di derivata destra o sinistra.
Se una funzione f è derivabile in un punto c, allora la funzione dfc:R→R, dfc(x)=f'(c)x si dice differenziale di f nel punto c. Si noti che la scrittura df costituisce un simbolo unico.
Esempio 1. Sia ![]() e
sia c un punto del dominio (c≥0). Si
può allora scrivere (se c=0 si intende che il
limite va preso solo da destra):
e
sia c un punto del dominio (c≥0). Si
può allora scrivere (se c=0 si intende che il
limite va preso solo da destra):
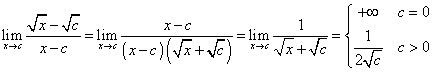 .
.
Pertanto la funzione radice risulta non derivabile per
c=0, mentre ha per derivata il numero ![]() per c>0. Si osservi che la funzione per
c=0 ha una tangente verticale in quanto inversa del
ramo di parabola y=x2 che sta nel primo
quadrante.
per c>0. Si osservi che la funzione per
c=0 ha una tangente verticale in quanto inversa del
ramo di parabola y=x2 che sta nel primo
quadrante.
Esempio 2. Sia f(x)=sgn(x) e sia c un reale non nullo. Poiché nel calcolo del limite intervengono solo i valori in un intorno di c, potremo tranquillamente supporre x non nullo e concorde a c. Allora:
-
se c>0 si ha
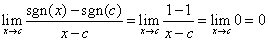 ;
;
-
se c<0 si ha
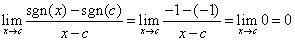 .
.
Pertanto la funzione è derivabile per c non
nullo e la sua derivata vale 0. La cosa era quasi ovvia
perché in un intorno di un punto c non nullo la
funzione è un segmento orizzontale che ha, ovviamente,
tangente orizzontale. Se c=0 si ha invece: 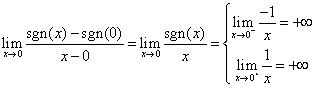 . Pertanto la funzione non è derivabile in
0 (secondo la definizione che abbiamo dato noi non ha derivata
in 0; si potrebbe anche dire che la funzione ha derivata in 0, e
che la derivata è infinita, ma resta comunque non
derivabile).
. Pertanto la funzione non è derivabile in
0 (secondo la definizione che abbiamo dato noi non ha derivata
in 0; si potrebbe anche dire che la funzione ha derivata in 0, e
che la derivata è infinita, ma resta comunque non
derivabile).
![]() Si
osservi che, graficamente, la situazione è completamente
diversa dall'esempio precedente e non si può ritenere
che la funzione signum abbia una tangente verticale:
è per questo motivo che, nel dare la definizione formale
di tangente, abbiamo escluso il caso che il limite del rapporto
incrementale possa essere infinito.
Si
osservi che, graficamente, la situazione è completamente
diversa dall'esempio precedente e non si può ritenere
che la funzione signum abbia una tangente verticale:
è per questo motivo che, nel dare la definizione formale
di tangente, abbiamo escluso il caso che il limite del rapporto
incrementale possa essere infinito.
Esempio 3. Sia f(x)=|x|. É
facile provare che se c non è nullo la derivata
è +1 (c>0) o -1 (c<0). Per
c=0 il limite del rapporto incrementale non esiste
perché ![]() . La situazione è
ancora diversa dalla precedente e questa volta esistono finiti i
limiti destro e sinistro del rapporto incrementale, in
corrispondenza di c=0, ma sono diversi: la funzione ha,
come preciseremo meglio in seguito, un punto angoloso.
. La situazione è
ancora diversa dalla precedente e questa volta esistono finiti i
limiti destro e sinistro del rapporto incrementale, in
corrispondenza di c=0, ma sono diversi: la funzione ha,
come preciseremo meglio in seguito, un punto angoloso.
La funzione derivata
Se una funzione f è derivabile in un certo
sottoinsieme A del suo dominio, si può considerare la
funzione che ad ogni punto di A fa corrispondere la derivata
della funzione in quel punto: la chiameremo la funzione derivata di f, e,
naturalmente, la indicheremo con f'. Per esempio se
riesaminiamo la funzione radice quadrata dell'esempio 1,
possiamo affermare che la sua funzione derivata è la
funzione, definita sui reali maggiori di zero, ![]() . Si badi bene, come mostra questo esempio, che il
dominio della funzione derivata può essere più
piccolo di quello della funzione originale.
. Si badi bene, come mostra questo esempio, che il
dominio della funzione derivata può essere più
piccolo di quello della funzione originale.
Continuità delle funzioni derivabili
Una prima, importantissima, proprietà delle funzioni derivabili è espressa dal seguente:
![]() Teorema: Se esiste la derivata
f'(c) di una funzione f in un punto
c, allora la funzione è continua in c.
Teorema: Se esiste la derivata
f'(c) di una funzione f in un punto
c, allora la funzione è continua in c.
La dimostrazione è immediata: si ha ![]() ,
da cui f è continua in c.
,
da cui f è continua in c.
Osservazioni importanti
- Si noti, nella dimostrazione precedente, che è fondamentale che f'(c) sia finito per poter concludere. In effetti gli esempi 1 e 2 precedenti provano che se il limite del rapporto incrementale è infinito una funzione può essere continua (la radice quadrata nell'origine), ma anche discontinua (la funzione signum).
- Si noti anche che l'esempio 3 qui sopra mostra che non è vero il viceversa di questo teorema: la funzione valore assoluto è continua nell'origine senza essere ivi derivabile. É possibile fornire esempi anche più complessi di funzioni che sono continue ovunque e giammai derivabili, ma questi esempi esulano dallo scopo di questa monografia. In ogni caso non è difficile immaginare curve continue e prive di tangente in ogni punto: un esempio classico è il fiocco di neve. Questa curva però non è il grafico di una funzione.