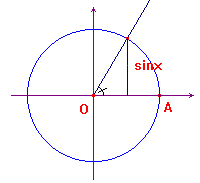Un segmento lungo √n, data l'unità
Si tratta di un problema elementare, ma importante nelle applicazioni. Si deve utilizzare ripetutamente il teorema di Pitagora.
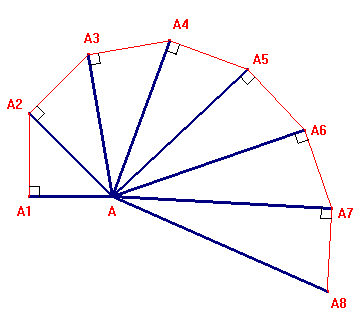
Nella figura qui sotto AA1 e tutti i segmenti rossi sono
l'unità di misura. Le ipotenuse dei triangoli
rettangoli costruiti in successione sono lunghe,
rispettivamente, 
. E' chiaro che, nella
costruzione, non si deve partire dal segmento lungo 1, basta
partire dal quadrato perfetto immediatamente precedente quello
richiesto. Per esempio per costruire la 
basta
partire da un triangolo rettangolo di cateti 6 e 1: si ottiene
prima 
e poi .
Una applicazione importante di questa tecnica si ha nella
costruzione di un angolo di seno (o coseno, tangente ...)
assegnato. Naturalmente la costruzione è possibile con
riga e compasso solo se il valore dato del seno è
costruibile. Nelle applicazioni interessa il caso 
.
Per risolvere il problema basta costruire il segmento 
(dove abbiamo razionalizzato il denominatore), a partire
dal raggio della circonferenza goniometrica, e riportarlo come
indicato in figura.
