Iterazioni e funzioni lineari
Il caso delle definizioni ricorsive definite da una funzione del tipo an+1=f(an), si presta ad interessanti considerazioni grafiche che hanno applicazioni anche nella cosiddetta "teoria del caos".
L'osservazione fondamentale è che, dato a0, si ottiene a1=f(a0), a2=f(a1)=f(f(a0))=(f°f)(a 0), ... an=(f°f°f°... °f)(a0), dove l'operazione di composizione va eseguita n volte. Si tratta in sostanza di iterare la funzione f. Per questo motivo a volte queste successioni si dicono anche successione iterative. E' chiaro che la successione ottenuta dipende dal valore di a0 e dalla funzione f data.
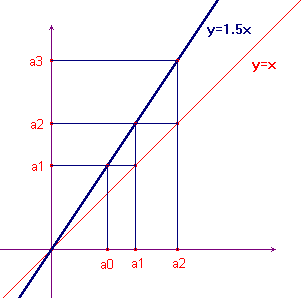Consideriamo l'esempio della definizione di potenza
di un dato numero k, dove a0=1 e
f(x)=k.x: si tratta di un esempio
particolarmente semplice in quanto la funzione f
è lineare.
Rappresentiamo in un sistema cartesiano xOy la funzione
f(x)=kx, e la bisettrice y=x. Per fissare le
idee scegliamo k=1.5. Avremo una retta passante per
l'origine e di pendenza m=1.5. A partire da
a0=1 otteniamo a1
utilizzando il grafico di y=1.5x; riportato
a1 sull'asse delle ascisse utilizzando
una simmetria rispetto alla bisettrice y=x, otteniamo
a2, e successivamente, con lo stesso
procedimento, tutti gli altri.
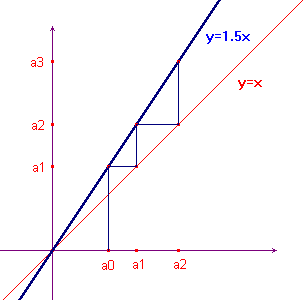Risulta abbastanza evidente che nel grafico di sopra si
possono potare un bel po' di rami secchi. lasciando solo i
tratti riportati qui a fianco. Si ottiene una specie di
scaletta.
Il grafico a lato rende evidente che, al crescere di n,
an diverge verso +∞.
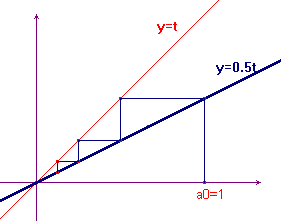Se
consideriamo un k<1, esempio k=0.5, come
nella figura qui a lato, dove abbiamo rappresentato solo i rami
non potati, troviamo che, al crescere di n,
an tende a zero. Anche qui si ottiene una
specie di scaletta. però discendente verso lo zero.
Non è difficile vedere quello che succede se k=1
oppure k=0.
Consideriamo ora valori di k negativi. Le rette che rappresentano la funzione f sono decrescenti e il grafico assume un aspetto completamente diverso: le scalette sono sostituite da "ragnatele". Nelle figure qui sotto, a sinistra il caso k=-0.5, a destra il caso k=-1.5. Nel primo caso si ha convergenza verso zero, nel secondo caso i termini pari divergono a +∞, quelli dispari a -∞.
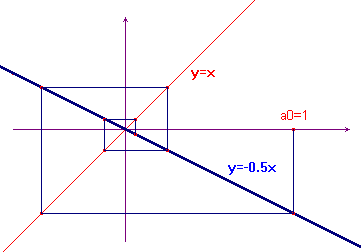
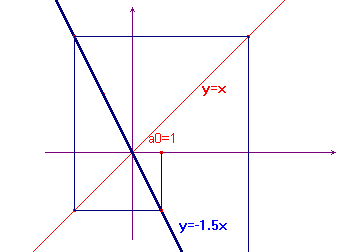
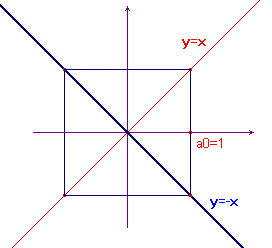
Il caso k=-1 è diverso dai precedenti in quanto la successione, al variare di n, passa e ripassa sempre per gli stessi due punti: -1 e 1.
Che cosa succederebbe se, mantenendo la stessa funzione
f(x)=k.x, usassimo un diverso valore
di a0? Consideriamo per esempio il
caso a0=2: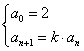 
. E' immediato che la successione sarebbe ora: {2,
2k, 2k2, 2k3,...}; si tratterebbe solo di
un cambiamento di scala, senza quindi sostanziale differenza per
quanto riguarda la "tendenza al limite".
Situazioni più interessanti si ottengono prendendo altre funzioni e considereremo ora alcuni esempi.